Der Rückschaufehler entsteht, wenn probabilistische Prognosevorhersagen und beobachtete Ist-Werte bei der Bewertung der Prognosegenauigkeit über verschiedene Verkaufsfrequenzen hinweg nicht richtig gruppiert werden. Zum einen ist der Rückschaufehler eine heimtückische Falle, die dazu verleitet, falsche Schlussfolgerungen über die Voreingenommenheit einer gegebenen Wahrscheinlichkeitsprognose zu ziehen – im schlimmsten Fall dazu, dass man sich für ein schlechteres Modell anstelle eines besseren entscheidet. Andererseits berühren ihre Lösung und Erklärung statistische Grundlagen wie die Repräsentativität der Stichprobe, die Wahrscheinlichkeitsprognose, bedingte Wahrscheinlichkeiten, die Regression zum Mittelwert und die Bayes-Regel. Darüber hinaus regt es uns zum Nachdenken darüber an, was wir intuitiv von einer Prognose erwarten und warum das nicht immer angemessen ist.
Wettervorhersagen können sich auf einzelne Kategorien beziehen – wird es morgen ein Gewitter geben? — oder kontinuierliche Größen — wie hoch wird die Höchsttemperatur morgen sein? Wir konzentrieren uns hier auf einen Hybridfall: Diskrete Größen, wie zum Beispiel die Anzahl der T-Shirts, die an einem bestimmten Tag verkauft werden. Bei einer solchen Verkaufszahl handelt es sich um eine diskrete Zahl; sie könnte 0, 1, 2, 13 oder 56 sein; aber sicherlich nicht -8,5 oder 3,4. Unsere Prognose ist probabilistisch; wir können nicht genau vorhersagen, wie viele T-Shirts verkauft werden. Ein realistischer, aber ambitioniert enger (d.h. Die präzise Wahrscheinlichkeitsverteilung ist die Poisson-Verteilung. Wir gehen daher davon aus, dass unsere Prognose die Poisson-Rate liefert, die unserer Ansicht nach den tatsächlichen Verkaufsprozess bestimmt.
Eine eher mittelmäßige Prognose?
Angenommen, die Prognose wurde erstellt, die tatsächlichen Verkaufszahlen wurden erfasst und die Prognose wird anhand der folgenden Tabelle ausgewertet:
| Beobachtete Verkaufshäufigkeit | Durchschnittliche beobachtete Verkäufe | Mittlere Vorhersage |
| Langsam 0, 1, 2 Stück/Tag | 0,804 | 1,373 |
| Medium 3-10 Stück/Tag | 5.119 | 4.601 |
| Schnell >10 Stück/Tag | 13.880 | 11.041 |
Die Daten werden nach der beobachteten Verkaufshäufigkeit gruppiert: Wir teilen alle Tage in Gruppen ein, in denen das T-Shirt wenige (0, 1 oder 2), mittlere (3 bis 10) oder viele (mehr als 10) Male verkauft wurde. Auf den ersten Blick schreit diese Tabelle unmissverständlich: „Langsam verkaufende Produkte werden überbewertet, schnell verkaufende Produkte unterbewertet.“ Die Prognose ist so offensichtlich fehlerhaft, dass wir sofort versuchen würden, sie zu korrigieren, oder etwa nicht?
Tatsächlich ist, und das mag überraschend klingen, alles in Ordnung. Ja, langsam verkaufende Artikel werden tatsächlich überbewertet und schnell verkaufende Artikel unterbewertet, aber die Prognose verhält sich genau so, wie sie sollte. Fehlerhaft ist unsere Erwartung, dass die Spalten „mittlere beobachtete Verkäufe“ und „mittlere Prognose“ übereinstimmen sollten. Wir haben es mit einem psychologischen Problem zu tun, mit unserer unrealistischen Erwartung, und nicht mit einer schlechten Prognose! Eine Wahrscheinlichkeitsprognose hat nie versprochen und wird auch nie garantieren, dass für jede mögliche Gruppe von Ergebnissen der Mittelwert der Prognose mit dem Mittelwert des Ergebnisses übereinstimmt.
Lasst uns untersuchen, warum das so ist, wie dieses Problem zufriedenstellend gelöst werden kann und wie ähnliche Verzerrungen vermieden werden können.
Was genau fordern wir?
Lassen Sie uns einen Schritt zurücktreten und in Worten ausdrücken, was die Tabelle offenbart. Die Daten werden anhand der tatsächlich beobachteten Verkäufe kategorisiert, das heißt, wir filtern oder bedingen die Vorhersagen und die Beobachtungen danach, ob die Beobachtungen in einem bestimmten Bereich liegen (langsame, mittlere oder schnelle Verkäufer). Die erste Zeile enthält alle Tage, an denen das T-Shirt 0, 1 oder 2 Mal verkauft wurde, die mittlere Spalte liefert uns:

d. h. der Mittelwert der Beobachtungen in der Gruppe, in die wir alle Beobachtungen mit dem Wert 2, 1 oder 0 zusammengefasst haben – definitiv eine Zahl zwischen 0 und 2, die zufällig 0,804 beträgt. Die rechte Spalte enthält die erwartete mittlere Vorhersage für denselben Beobachtungsbereich.

Das heißt, für alle Beobachtungen, die 2 oder weniger betragen, nehmen wir die entsprechende Vorhersage und berechnen den Mittelwert über alle diese Vorhersagen.
A priori gibt es keinen Grund, warum der erste und der zweite Ausdruck denselben Wert annehmen sollten – aber intuitiv würden wir uns das wünschen: Zu erwarten, dass die mittlere Vorhersage der mittleren Beobachtung entspricht, scheint nicht zu viel verlangt zu sein, oder?
| Beobachtete Verkaufshäufigkeit | Durchschnittliche beobachtete Verkäufe | Mittlere Vorhersage |
| Langsam 0, 1, 2 Stück/Tag | E (Beobachtung | Beobachtung ≤ 2) | E (Vorhersage | Beobachtung ≤ 2) |
| Medium 3-10 Stück/Tag | E (Beobachtung | Beobachtung ≤ 3, ≤ 10 ) | E (Vorhersage | Beobachtung ≤ 3, ≤ 10] ) |
| Schnell >10 Stück/Tag | E (Beobachtung | Beobachtung ≥ 11) | E (Vorhersage | Beobachtung ≥ 11]) |
Vorausschauende Prognose, rückblickende Erkenntnis
Entsprechend ihrer Etymologie sind Prognosen zukunftsorientiert und liefern uns Wahrscheinlichkeiten, um zukünftige Ergebnisse zu beobachten.
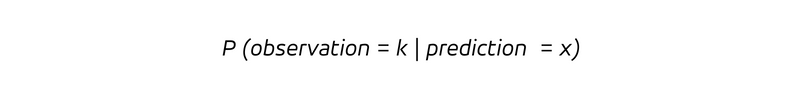
Dies ist die bedingte Wahrscheinlichkeit, ein Ergebnis k zu beobachten, vorausgesetzt, die vorhergesagte Rate ist x. Da wir eine bedingte Wahrscheinlichkeit haben, betrachten wir die Wahrscheinlichkeitsverteilung für die Beobachtungen unter der Annahme, dass die Vorhersage den Wert x angenommen hat. Bei einer unverzerrten Prognose ist der Erwartungswert der Beobachtung unter der Bedingung einer Vorhersage x, d. h. der Mittelwert der Beobachtung unter der Annahme einer Vorhersage mit dem Wert x, wie folgt:
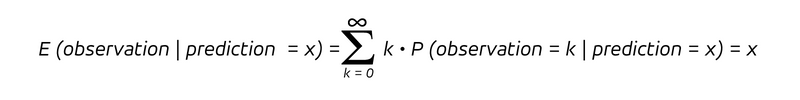
Das ist es, was jede unvoreingenommene Prognose verspricht: Wenn man alle Vorhersagen mit dem gleichen Wert x gruppiert, sollte der Mittelwert der resultierenden Beobachtungen sich genau diesem Wert x annähern. Die Verteilung kann zwar viele verschiedene Formen annehmen, diese Eigenschaft ist jedoch von grundlegender Bedeutung.
Werfen wir einen Blick zurück auf die Tabelle: Was wir in der linken Spalte tun, ist nicht die Gruppierung/Konditionierung nach Vorhersage, sondern nach Ergebnis. Die rechte Spalte fragt daher rückwärtsgerichtet „Was war unsere mittlere Vorhersage bei einem bestimmten Ergebnis k?“ anstatt zukunftsgerichtet „Was wird das mittlere Ergebnis sein bei unserer Vorhersage x?“.
Um eine rückwärtsgewandte Aussage in Bezug auf eine zukunftsorientierte Aussage auszudrücken, wenden wir die Bayes-Regel an.

Die rückwärts- und zukunftsorientierten Fragen sind unterschiedlich, und so sind auch ihre Antworten: Es tauchen weitere Begriffe auf, P (Vorhersage = x) und P (Beobachtung = k), die unbedingten Wahrscheinlichkeiten für eine Vorhersage und ein Ergebnis. Folglich ergibt sich der Erwartungswert der mittleren Vorhersage bei einem bestimmten Ergebnis zu:

Minimalistisches Beispiel
Welchen Wert nimmt E (Vorhersage | Beobachtung = m) an? Warum sollte es sich nicht einfach auf die Beobachtung m vereinfachen?
In der überwiegenden Mehrheit der Fälle gilt : E (Vorhersage | Beobachtung = m) ≠ m. Mal sehen, warum!
Betrachten wir ein T-Shirt, das sich jeden Tag gleich gut verkauft und einer Poisson-Verteilung mit der Rate 5 folgt. Der gleiche prognostizierte Wert von 5 gilt für jeden Tag. Das Ergebnis ist jedoch unterschiedlich. Offensichtlich ist 5 eine Überschätzung für Ergebnisse 4 und niedriger und eine Unterschätzung für Ergebnisse 6 und höher. Wenn wir erneut nach Ergebnissen gruppieren, erhalten wir Folgendes:
| Beobachtete Verkaufshäufigkeit | Durchschnittliche beobachtete Verkäufe | Mittlere Vorhersage |
| Langsam <5 Stück/Tag | 3,0082 | 5 |
| Medium 5 Stück/Tag | 5 | 5 |
| Schnell >5 Stück/Tag | 7,2844 | 5 |
Aus dieser Tabelle schließen wir erneut, dass die Tage mit schwachen Verkäufen überschätzt und die Tage mit starken Verkäufen unterschätzt wurden, und das war auch tatsächlich so. Dies gilt für jede Beobachtung E (Vorhersage | Beobachtung = m) = 5, da die Vorhersage immer 5 ist.
Die Prognose ist nach wie vor „perfekt“ – die Ergebnisse verhalten sich genau wie vorhergesagt, sie folgen der Poisson-Verteilung mit der Rate 5. Der Eindruck einer Unter- bzw. Überprognose ist ausschließlich eine Folge der Datenauswahl: Durch die Auswahl der Ergebnisse über 5 behalten wir diejenigen Ergebnisse, die über dem Prognosewert von 5 liegen und unterschätzt wurden; durch die Auswahl der Ergebnisse unter 5 behalten wir die Ereignisse, die unter dem Prognosewert von 5 liegen und überschätzt wurden. Bei einer Wahrscheinlichkeitsprognose ist es unvermeidlich, dass einige Ergebnisse unterschätzt und andere überschätzt wurden. Unter der Annahme, dass die Prognose unvoreingenommen ist, gehen wir davon aus, dass sich Unter- und Überprognosen bei einer gegebenen Vorhersage m ausgleichen. Wir können nicht erwarten, dass die von uns aktiv ausgewählten über- bzw. unterschätzten Beobachtungen dann nicht über- bzw. unterschätzt sind!
In einer realistischen Situation werden wir es nicht mit einer Prognose zu tun haben, die für jeden Tag denselben Wert annimmt, sondern die Vorhersage selbst wird variieren. Dennoch läuft die Auswahl von „eher großen“ oder „eher kleinen“ Ergebnissen darauf hinaus, die unter- bzw. überschätzten Ereignisse in den Kategorien zu belassen. Daher gilt allgemein E (Vorhersage | Beobachtung = m) ≠ m . Genauer gesagt, immer wenn m so groß ist, dass die Auswahl von m gleichbedeutend mit der Auswahl unterprognostizierter Ereignisse ist, dann gilt E (Vorhersage | Beobachtung = m) < m; wenn m ausreichend klein ist, dass die Auswahl von m gleichbedeutend mit der Auswahl überprognostizierter Ereignisse ist, dann gilt E (Vorhersage | Beobachtung = m) > m.
Deterministische Prognosen – das hättest du schon immer wissen müssen!
Warum ist das für uns rätselhaft? Warum empfinden wir diese Diskrepanz zwischen durchschnittlicher Beobachtung und durchschnittlicher Prognose als unangenehm? Unsere Intuition beruht auf der Übereinstimmung von Vorhersage und Beobachtung, die deterministische Prognosen kennzeichnet. In der Sprache der Wahrscheinlichkeiten drückt eine deterministische Vorhersage Folgendes aus: P (Beobachtung = Vorhersage) = 1 und P (Beobachtung ≠ Vorhersage) = 0
Die Prognostikerin geht davon aus, dass die Beobachtung exakt mit ihrer Vorhersage übereinstimmt, d. h. vorhergesagte und beobachtete Werte stimmen mit einer Wahrscheinlichkeit von 1 (oder 100 %) überein, während alle anderen Ergebnisse als unmöglich angesehen werden. Das ist eine selbstbewusste, um nicht zu sagen, eine gewagte Aussage. Ausgedrückt durch bedingte Wahrscheinlichkeiten lässt sich Folgendes zusammenfassen:

In Worten ausgedrückt: Immer wenn wir vorhersagen, k Stücke zu verkaufen (die Bedingung nach dem senkrechten Strich), werden wir k Stücke verkaufen. Da der Determinismus nicht nur impliziert, dass wir jedes Mal, wenn wir k vorhersagen, auch k beobachten, sondern auch, dass jede Beobachtung k ex ante korrekt als k vorhergesagt wurde, gilt:
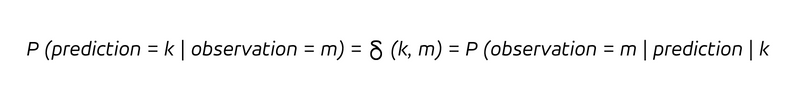
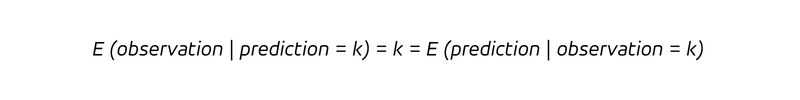
Der Determinismus macht die Unterscheidung zwischen rückwärtsgewandten und zukunftsorientierten Fragen überflüssig. Bei einer deterministischen Prognose lernen wir durch die Beobachtung des Ergebnisses nichts Neues (wir wussten es ja schon!), und wir würden unsere Überzeugung nicht aktualisieren (die ja bereits richtig war).
Bei einer derart deterministischen Prognose, bei der alle scheinbaren Wahrscheinlichkeitsverteilungen auf einen Höchstwert von 100 % beim einzig möglichen Ergebnis zusammenfallen, tritt keine Verzerrung durch nachträgliche Selektion auf – wir tun so, als hätten wir es vorher genau gewusst, also hätten wir es auch wissen müssen – immer und unter allen Umständen. Wenn die Messung etwas anderes sagt, ist Ihre „deterministische“ Prognose falsch.
Jede seriöse Prognose ist probabilistisch.
Wahrscheinlichkeitsprognosen sind weniger aussagekräftig als deterministische Prognosen, und für Wahrscheinlichkeitsprognosen müssen wir die Vorstellung aufgeben, dass jedes Ergebnis m im Durchschnitt als m vorhergesagt wurde – deterministische Prognosen erscheinen daher sehr attraktiv. Aber ist es realistisch, den täglichen T-Shirt-Absatz deterministisch vorherzusagen? Nehmen wir an, Sie wären dazu in der Lage und prognostizieren für morgen einen T-Shirt-Absatz von 5. Das bedeutet, dass Sie fünf Personen nennen können, die, egal was passiert (Unfall, Krankheit, Gewitter, plötzlicher Sinneswandel…), morgen ein rotes T-Shirt kaufen werden. Wie können wir erwarten, ein solches Maß an Gewissheit zu erreichen? Warst du dir jemals so sicher, dass du am nächsten Tag ein rotes T-Shirt kaufen würdest? Selbst wenn fünf Freunde versprechen, dass sie morgen unter allen Umständen ein T-Shirt kaufen würden – wie könnte man ausschließen, dass jemand anderes unter all den anderen potenziellen Kunden ebenfalls ein T-Shirt kaufen würde? Abgesehen von einigen sehr ungewöhnlichen Sonderfällen (sehr wenige Kunden, Lagerbestand ist viel kleiner als die tatsächliche Nachfrage), ist eine deterministische Vorhersage der genauen Verkaufszahlen eines Artikels ausgeschlossen. Unsicherheit lässt sich nur bis zu einem gewissen Grad bändigen, und jede realistische Prognose ist eine Wahrscheinlichkeitsprognose.
Evaluierungshygiene
Es gibt eine alternative Möglichkeit, Tabelle 1 zu widerlegen: Indem wir die Tabelle aufstellen, stellen wir eine statistische Frage, nämlich ob die Prognose verzerrt ist oder nicht und in welche Richtung (ignorieren wir für den Moment die Frage der statistischen Signifikanz und nehmen wir an, dass jedes Signal, das wir sehen, statistisch signifikant ist). Wie jede statistische Analyse kann auch eine Prognoseanalyse Verzerrungen unterliegen. Die Art und Weise, wie wir anhand der Ergebnisse ausgewählt haben, ist ein Paradebeispiel für die Selektionsverzerrung: Die Ereignisse in der Gruppe „langsame Verkäufer“, „mittlere Verkäufer“, „schnelle Verkäufer“ sind nicht repräsentativ für die Gesamtheit der Vorhersagen und Beobachtungen, sondern wir haben sie in die Unter- und Überprognosekategorien eingeteilt. Darüber hinaus haben wir bei der Prognoseauswertung sogenannte „Zukunftsinformationen“ verwendet: Die Kategorien, in die wir Vorhersagen und Beobachtungen eingeteilt haben, sind zum Zeitpunkt der Prognose noch nicht definiert, sondern werden erst im Nachhinein festgelegt. Die Art und Weise, wie wir die Tabelle aufgebaut haben, verstößt somit gegen grundlegende Prinzipien statistischer Analysen.
Regression zum Mittelwert
Das Phänomen, das wir gerade erlebt haben – dass extreme Ereignisse nicht so extrem vorhergesagt wurden, wie sie sich letztendlich herausstellten – steht in direktem Zusammenhang mit der „Regression zum Mittelwert“, einem statistischen Phänomen, für das wir nicht einmal eine Prognose benötigen: Angenommen, Sie beobachten eine Zeitreihe von Verkäufen eines Produkts, die keine Saisonalität oder andere zeitabhängige Muster aufweist. Wenn die beobachteten Umsätze an einem bestimmten Tag höher sind als die durchschnittlichen Umsätze, können wir ziemlich sicher sein, dass die beobachteten Umsätze am nächsten Tag niedriger sein werden als die heutigen, und umgekehrt. Wenn wir einen sehr großen oder sehr kleinen Wert wählen, wählen wir aufgrund der Wahrscheinlichkeitsnatur des Prozesses wahrscheinlich eine positive oder negative Zufallsschwankung aus, und die Verkaufszahlen werden sich schließlich wieder dem Mittelwert annähern. Psychologisch gesehen neigen wir dazu, diese Regression zur Mitte – ein rein statistisches Phänomen – kausal einer aktiven Intervention zuzuschreiben.
Lösung: Gruppierung nach Vorhersage, nicht nach Ergebnis. Achten Sie stets auf mögliche Selektionsverzerrungen.
Wie lässt sich dieses Dilemma lösen? Durch die Gruppierung nach Ergebnissen wählen wir im Hinblick auf ihre Prognose eher „große“ oder „eher kleine“ Werte aus – wir erhalten keine repräsentative Stichprobe, sondern eine verzerrte. Diese Selektionsverzerrung führt zu Kategorien, die Ergebnisse enthalten, die naturgemäß eher „unterschätzt“ bzw. eher „überschätzt“ sind. Wir leiden unter dem Rückschaufehler, wenn wir glauben, dass der Mittelwert der Vorhersage und der Mittelwert der Beobachtung bei sich „langsam“, „mittel“ und „schnell“ bewegenden Elementen gleich sein sollten. Wir müssen mit der Diskrepanz zwischen den beiden Spalten leben und sie akzeptieren. Zum Glück können wir den Satz von Bayes verwenden, um den realistischen Erwartungswert zu erhalten. Eine Lösung wäre demnach eine weitere Spalte in der Tabelle, die den theoretisch erwarteten Wert der mittleren Vorhersage pro Bucket enthält, welcher mit der tatsächlichen mittleren Vorhersage in diesem Bucket verglichen werden kann. Das heißt, wir können den Rückschaufehler quantifizieren und theoretisch reproduzieren und sehen, ob die aggregierten Daten der theoretischen Erwartung entsprechen.
Eine wesentlich einfachere Lösung besteht jedoch darin, andere Fragen an die Daten zu stellen, nämlich Fragen, die mit dem übereinstimmen, was die Prognose uns verspricht. Dies erlaubt uns, direkt zu überprüfen, ob diese Versprechen erfüllt werden oder nicht: Anstatt nach Ergebniskategorien zu gruppieren, gruppieren wir nach Vorhersagekategorien, d. h. nach vorhergesagten langsamen, mittleren und schnellen Verkäufern. Hier können wir überprüfen, ob die Prognoseversprechen (der durchschnittliche Umsatz bei einer bestimmten Vorhersage entspricht dieser Vorhersage) erfüllt werden. Für unser Beispiel erhalten wir folgende Tabelle:
| Prognostizierte Verkaufshäufigkeit | Durchschnittliche beobachtete Verkäufe | Mittlere Vorhersage |
| Langsam <3 Stück/Tag | 1.288 | 1.267 |
| Medium 3 Stück/Tag | 5.247 | 5.229 |
| Schnell >3 Stück/Tag | 12.855 | 12.950 |
Unter Berücksichtigung der Gesamtzahl der Messungen wäre ein Test auf statistische Signifikanz negativ, d. h. es würde kein signifikanter Unterschied zwischen dem durchschnittlichen beobachteten Umsatz und der durchschnittlichen Vorhersage festgestellt. Wir kommen zu dem Schluss, dass unsere Prognose nicht nur global unvoreingenommen ist, sondern auch pro Prognoseschicht unvoreingenommen.
Im Allgemeinen kann man eine Prognose bewerten, indem man alle zum Vorhersagezeitpunkt bekannten Informationen filtert, und die Prognose sollte in allen Tests unvoreingenommen sein. Allerdings darf der Filter keine zukünftigen Informationen enthalten, wie zum Beispiel zufällige Schwankungen in den Beobachtungen, über die die Natur erst zum Zeitpunkt der Vorhersage entscheidet.
Was sollten Sie mitnehmen, wenn Sie es bis hierher geschafft haben? (1) Wenn Sie nach Ergebnis auswählen, erhalten Sie keine repräsentative Stichprobe. (2) Seien Sie skeptisch gegenüber Ihren eigenen Erwartungen – sehr vernünftig erscheinende intuitive Erwartungen erweisen sich oft als fehlerhaft. (3) Formulieren Sie Ihre Erwartungen explizit und überprüfen Sie sie anhand gut verstandener Fälle.













