Bei der Bedarfsprognose im Einzelhandel ist die relevante Größe die Kundennachfrage nach einem bestimmten Produkt, z. B. wie viele Körbe Erdbeeren nachgefragt werden. In der Praxis beobachtet man eine etwas, aber dennoch signifikant abweichende Größe, nämlich die registrierten Umsätze. Der Absatz spiegelt die Nachfrage wider, ist aber durch die Kapazität, d. h. den Lagerbestand, begrenzt: Wenn 20 Warenkörbe nachgefragt werden, aber nur 12 verfügbar sind, werden nur 12 verkauft, und die 8 Kunden, die ebenfalls kaufen wollten, konnten nicht bedient werden. Die Unterscheidung zwischen Umsatz und Nachfrage mag wie Haarspalterei erscheinen, aber dieser Blogbeitrag zeigt Ihnen, warum die Verwechslung von Umsatz und Nachfrage zu voreingenommenen Schulungen und fehlerhaften Modellevaluierungen führt. Sie erfahren, wie sich begrenzte Lagerbestände auf den Umsatz auswirken und wie Sie die wichtigsten Fallstricke umgehen können, um Situationen aus der Praxis, in denen begrenzte Lagerbestände eine Rolle spielen, souverän zu meistern.
Nachfrage und Absatz
Was ist die präziseste Prognose, die Ihnen einfällt, eine stets zutreffende Nachfragevorhersage, auf die man sich in jeder Situation verlassen kann? In vielen Situationen lautet die Antwort: Einfach immer „0“ vorhersagen! Bei einer Nachfrageprognose von Null wird kein einziger Artikel bestellt, es werden keine Artikel im Regal stehen und es wird kein Artikel verkauft. Die Nullprognose erwies sich als goldrichtig und stimmte perfekt mit den beobachteten Nullverkäufen überein. Diese absolut zutreffende Vorhersage ist natürlich nicht die Prognose, die Ihren Vorgesetzten freuen wird.
Dieses extreme Beispiel verdeutlicht, dass man vorsichtig sein sollte, was man verlangt: Das Ziel eines Einzelhändlers ist nicht die Erstellung einer präzisen Prognose, sondern der Betrieb eines nachhaltigen Unternehmens. Das Paradoxon offenbart auch ein grundlegendes Dilemma bei der Nachfrageprognose: Die Prognose selbst beeinflusst den letztendlich bereitgestellten Lagerbestand und gefährdet damit dessen Bewertung. Man könnte argumentieren, dass dieser Einfluss aus guten Gründen existiert, schließlich wurde die Prognose genau dafür erstellt! Der Lagerbestand setzt jedoch eine Obergrenze für die Anzahl der verkaufbaren Artikel, was die beobachtbaren Verkaufswerte künstlich einschränkt. Dies führt zu einer Diskrepanz zwischen der hypothetischen Nachfrage („wie viel nachgefragt wird“) und den tatsächlich erzielten Verkäufen („wie viel verkauft wurde“). Die beobachteten Umsätze entsprechen entweder der tatsächlichen Nachfrage oder den verfügbaren Lagerbeständen, je nachdem, welcher Wert niedriger ist.
In diesem Blogbeitrag werde ich Sie davon überzeugen, dass es keinen Weg an einer strengen probabilistischen Behandlung des Problems von Nachfrage versus Absatz vorbeiführt. Die Unterscheidung zwischen Nachfrage und Absatz, die sorgfältige Behandlung dieser Größen und dessen, was wir genau vorhersagen und beobachten, ist der Schlüssel für ein erfolgreiches und korrektes Modelltraining und eine korrekte Modellbewertung.
Um das Ganze greifbar (und schmackhaft) zu machen, betrachten wir einen Einzelhändler, der Körbe mit frischen Erdbeeren verkauft. Die ganzzahlige Anzahl der verkauften Körbe kann dann als „Stück“ betrachtet werden. Leider verderben diese ultrafrischen Lebensmittel, wenn sie tagsüber nicht verkauft werden. Daher ist Überbestellung, also das Vorhalten von mehr Ware als bestellt wird, kostspielig und sollte vermieden werden. Stellen Sie sich andererseits vor, Sie hätten Lust auf Erdbeeren, aber diese sind bereits ausverkauft, wenn Sie in Ihrem örtlichen Supermarkt danach suchen: Sie werden zu einem frustrierten Kunden, dessen Zahlungsbereitschaft nicht ausgeschöpft wurde. Daher ist auch eine Unterbestellung, also das Vorhandensein von weniger Ware auf Lager als bestellt, kostspielig, sowohl im Hinblick auf die Kundenzufriedenheit als auch auf Umsatz- und Gewinnverluste.
Ein Einzelhändler sollte die richtige Anzahl an Erdbeerkörben bestellen, um Verschwendung und Umsatzeinbußen sorgfältig auszugleichen. Um dieses Bestellproblem zu lösen, ist natürlich eine präzise Nachfrageprognose erforderlich, die tatsächlich vorhersagt, wie viele Warenkörbe angefragt werden und nicht, wie viele verkauft werden (denken Sie an die sich selbst erfüllende „0“-Prophezeiung oben).
Wie viel werden wir verkaufen?
Lasst uns die Nachfrageprognosen etwas genauer betrachten und ihre Bedeutung analysieren. Eine Bedarfsprognose gibt an, wie viele Artikel nachgefragt werden. Was genau bedeutet es aber, wenn „9,7 Körbe angefordert werden“? Offensichtlich kann man keine Bruchteilsmenge an Erdbeerkörben verkaufen, die wörtliche Auslegung ist lächerlich. Dennoch akzeptieren und verstehen wir die Prognose intuitiv und interpretieren sie als eine Aussage über die durchschnittliche erwartete Anzahl verkaufter Warenkörbe, die Anzahl der Warenkörbe, die wir im Durchschnitt verkaufen, wenn sich die gleiche Situation viele Male wiederholt (und die Lagerbestände immer ausreichend sind, wovon wir vorerst ausgehen). Daher verbirgt unsere Prognose implizit eine Wahrscheinlichkeitsverteilung, d. h. eine Vorstellung davon, wie wahrscheinlich es ist, 1, 2, 3, … Warenkörbe zu verkaufen, da sie nur den durchschnittlichen erwarteten Absatz angibt. Wie hoch diese Wahrscheinlichkeiten sind oder wie nahe die einzelnen Beobachtungen (d. h. die tatsächlichen Verkaufszahlen) an diesem Mittelwert von 9,7 liegen, wird nicht erwähnt.
Lasst uns den Teppich anheben, unter dem die Wahrscheinlichkeitsverteilung verborgen war, um zu sehen, wie sie aussehen sollte. Wir verwenden die untenstehende Grafik, um unser Beispiel zu veranschaulichen. Wahrscheinlichkeitsverteilungen mit einem Erwartungswert von 9,7 können a priori sehr unterschiedliche Formen annehmen: Man denke beispielsweise an eine Wahrscheinlichkeit von 51,5 %, auf Null zu stoßen, und eine Wahrscheinlichkeit von 48,5 %, 20 zu finden, wie im linken Teilbild dargestellt. Daraus ergibt sich ein Mittelwert von 9,7 – obwohl man nie einen Wert nahe 9,7 beobachtet, wie etwa 9 oder 10, sondern nur Extremwerte wie 0 oder 20. Die Wahrscheinlichkeitsverteilung des mittleren Diagramms weist der Zahl 10 eine Wahrscheinlichkeit von 70 % und der Zahl 9 eine Wahrscheinlichkeit von 30 % zu; sie weist außerdem den Erwartungswert 9,7 auf, jedoch konzentriert sich die Wahrscheinlichkeitsmasse viel stärker auf Werte nahe dem Mittelwert, der somit eine gute Schätzung für die typische Anzahl der Verkäufe darstellt. Die Menge der Verteilungen mit einem Mittelwert von 9,7 ist unendlich groß, und die meisten dieser Verteilungen sind ungeordnet (oder „pathologisch“, wie Mathematiker gerne sagen). Zum Glück können wir einfache und gutartige Wahrscheinlichkeitsverteilungen annehmen, wie zum Beispiel die Poisson-Verteilung im rechten Diagramm (lesen Sie den Blogbeitrag "Forecasting few is different", um zu erfahren, warum das eine vernünftige Wahl ist).
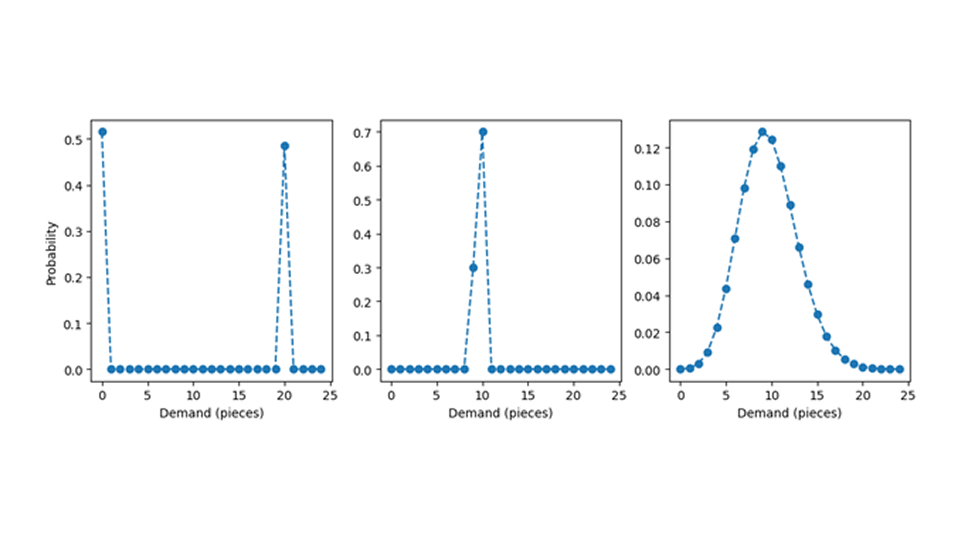
Im gesamten Text gehen wir davon aus, dass die Prognose den Mittelwert einer vorhergesagten Poisson-Verteilung liefert und dass die Nachfrage tatsächlich Poisson-verteilt ist, d.h. dass die Prognose korrekt ist. Selbst dieses idealisierte Szenario birgt genügend Feinheiten, um einen Blogbeitrag zu rechtfertigen.
Wie endliche Lagerbestände Informationen zensieren
Nun lassen wir die endliche Kapazität ins Spiel einfließen. Ausgehend von einer Nachfrageverteilung erhalten wir die Absatzverteilung, indem wir jedem möglichen Nachfragewert den entsprechenden Absatzwert zuordnen. Bei allen Nachfragewerten, die unter oder gleich der Anzahl der verfügbaren Bestände liegen, entspricht die Nachfrage einem Verhältnis von 1:1 zu den Verkäufen: Wenn 12 Körbe verfügbar sind, führen 5 angefragte Körbe zu 5 verkauften Körben, 12 angefragte Körbe führen zu 12 verkauften Körben. Wenn die Nachfrage größer ist als der Lagerbestand, also die Kapazität nicht ausreicht, sind die Verkäufe durch den Lagerwert begrenzt: Wenn 13, 25 oder 463 Warenkörbe angefragt werden, werden nur 12 verkauft. Wenn der gesamte Lagerbestand abverkauft wird, nennen wir dies ein „Kapazitätsengpass“-Ereignis. Die Wahrscheinlichkeitsmasse, die mit der Nachfrage nach 13, 25 oder 463 Warenkörben verbunden ist, muss jedoch „irgendwohin“ und wird effektiv zur Wahrscheinlichkeit addiert, dass die Gesamtmenge angefragt wird. Die Absatzwahrscheinlichkeitsverteilungen für eine mittlere Nachfrage von 9,7 und unterschiedliche Kapazitäten (16, 12, 8) sind in der nächsten Abbildung dargestellt.
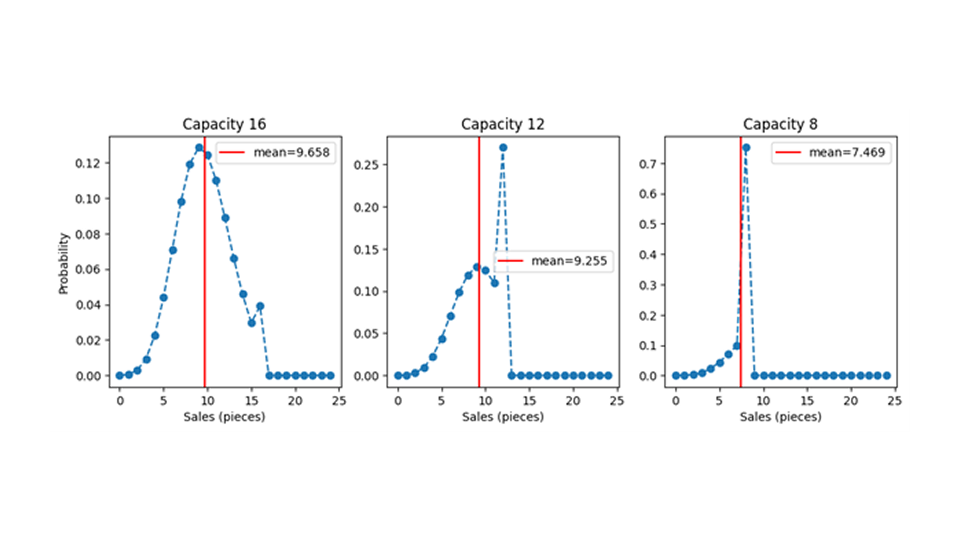
Die begrenzte Kapazität führt dazu, dass die Nachfrage auf eine Weise zensiert wird , die Informationen entfernt : Wenn man eine Kapazität von 16 Einheiten einrichtet und eine Kapazitätsauslastung, also 16 Verkäufe, beobachtet, kann man lediglich schließen, dass die Nachfrage mindestens 16 Einheiten betrug – nicht aber, ob sie 16, 25 oder 7.624 Einheiten betrug. Die tatsächliche Nachfrage hat einen Ihnen unbekannten Wert – sagen wir, 47 –, aber Sie beobachten nur 16. Aufgrund begrenzter Kapazitäten verlieren wir tatsächlich Informationen auf unwiderrufliche Weise (und das betrifft nicht nur die Kundenzufriedenheit). Dieser Informationsverlust erschwert sowohl das Trainieren von Modellen unter begrenzter Kapazität als auch deren Bewertung.
Die Diagramme zeigen außerdem die erwarteten durchschnittlichen Umsätze als vertikale rote Linien. Überraschenderweise hat die begrenzte Kapazität auch dann einen Einfluss auf den Erwartungswert des Umsatzes, wenn die Kapazität noch größer ist als die erwartete Nachfrage. Das heißt, wenn Sie eine Nachfrage von 9,7 prognostizieren und 12 Stück auf Lager haben, verkaufen Sie im Durchschnitt weniger als 9,7! Sie müssen im Durchschnitt mehr Ware einlagern als prognostiziert, um genauso viel zu verkaufen wie prognostiziert! Das könnte verwirrend sein: Bei einer einzelnen Veranstaltung entsprechen die Verkaufszahlen lediglich dem Minimum aus Nachfrage und Lagerbestand. Der Mittelwert der Absatzwahrscheinlichkeitsverteilung ist jedoch nicht unbedingt das Minimum der erwarteten Nachfrage und der Kapazität, da die Form der Wahrscheinlichkeitsverteilung berücksichtigt werden muss. Der Grund für dieses möglicherweise überraschende Verhalten liegt darin, dass der Wert der durchschnittlich prognostizierten Nachfrage auf Schwankungen um den Mittelwert beruht, die sich im Durchschnitt gegenseitig aufheben. Das heißt, die negativen Schwankungen (manchmal werden weniger als 9,7 Stück verkauft) werden durch die positiven Schwankungen (manchmal werden mehr als 9,7 Stück verkauft) ausgeglichen. Bei endlicher Kapazität werden die notwendigen positiven Schwankungen unterdrückt, und eine Aufhebung der positiven und negativen Schwankungen findet nicht mehr statt. Dies führt zu niedrigeren durchschnittlichen Umsatzerwartungen, selbst wenn die Kapazität größer ist als die durchschnittliche erwartete Nachfrage.
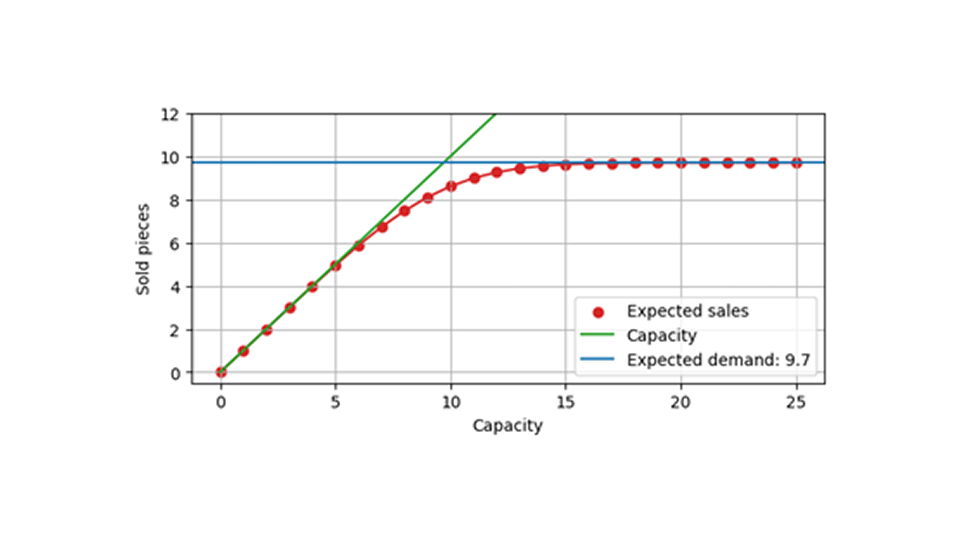
Die nachfolgende Grafik zeigt die erwarteten Umsätze in Abhängigkeit von der Kapazität, wiederum bei einer erwarteten Nachfrage von 9,7. Wenn die Kapazität viel größer ist als die erwartete Nachfrage (sagen wir, etwa 20), sind Ereignisse, die von der endlichen Kapazität betroffen sind, selten. Folglich bleibt die erwartete Absatzzahl unverändert und liegt weiterhin bei nahezu 9,7. Bei geringer Kapazität, beispielsweise 5, ist es fast unvermeidlich, dass die Kapazität erreicht wird, und im Durchschnitt wird ein Wert nahe dieser Kapazität verkauft. Zwischen etwa 7 und 14 Jahren findet ein Übergang statt; die Kapazität hat einen starken, aber nicht völlig bestimmenden Einfluss auf den Umsatz.
Training und Evaluierung von Modellen auf Basis zensierter Nachfrage
Nachdem wir nun unser Arbeitspferd – die Wahrscheinlichkeitsverteilung der Verkäufe, auch kapazitätszensierte Nachfrageverteilung genannt – unter Kontrolle haben, wollen wir verstehen, worauf wir beim Trainieren und Evaluieren von Modellen unter solchen Umständen achten müssen.
Wir müssen zwischen verschiedenen Regimen unterscheiden. Wenn die Kapazität jeden Tag erreicht würde, könnte man die wahre Nachfrage nie erfahren, sondern nur eine Untergrenze dafür („wir haben 5 Stück verkauft, also lag die Nachfrage bei mindestens 5“). Zum Glück ist dies ein unrealistisches Szenario: Wenn die Kapazität jeden Tag ausgeschöpft wird, haben wir es mit vielen unzufriedenen Kunden und einer großen unerfüllten Nachfrage zu tun – kein Einzelhändler kann eine solche Betriebsweise lange aufrechterhalten. Wenn sie aufgrund von Angebotsengpässen dazu gezwungen sind, könnten sie erwägen, die Nachfrage durch Preiserhöhungen zu steuern.
Im anderen Extremfall, wenn die Kapazität nie erreicht wird, genießen wir die angenehmen Bedingungen für Data Science: Wir lesen jeden Tag die tatsächliche Nachfrage ab und können im Grunde alle Diskussionen über die Kapazität vernachlässigen. Doch was für den Datenwissenschaftler ein Traum ist, ist für den Nachhaltigkeitsbeauftragten ein Albtraum: Eine solche Bestellstrategie würde zu einer enormen Menge an Abfall führen. Bei einer erwarteten Nachfrage von 9,7 müssten wir 21 Artikel auf Lager halten, um nur einmal in 1.000 Tagen ausverkauft zu sein.
Daher kommt es typischerweise vor, dass die Nachfrage manchmal die Kapazität erreicht (und das Produkt zu einem bestimmten Zeitpunkt im Laufe des Tages ausverkauft ist), und manchmal nicht (und am Abend noch einige Bestände vorhanden sind). Dies ist nachvollziehbar, da ein Kompromiss zwischen den widerstreitenden Zielen der Abfallvermeidung und der Vermeidung von Warenengpässen wünschenswert ist.
Wir sollten anerkennen, dass der Aufbau des bestmöglichen Modells im Widerspruch zum Betrieb des bestmöglichen Unternehmens steht: Bei einer nachhaltigen Geschäftsstrategie (bei der Abfall nicht völlig „frei“ ist, sondern zumindest bis zu einem gewissen Grad vermieden wird) ist es unvermeidlich, dass Produkte manchmal vergriffen sind. Die beste Datenanalyse findet jedoch dann statt, wenn garantiert ausgeschlossen ist, dass es jemals zu Warenengpässen kommt, und jeder Verkaufswert die Nachfrage direkt widerspiegelt. Da wir Data Science im Geschäftskontext betreiben, müssen wir mit einem Zwischenszenario und gelegentlichen Lieferengpässen leben.













