Im ersten Teil haben wir die übliche Methode zur Bestimmung des mittleren absoluten Fehlers in Frage gestellt, bei der einfach die Differenz zwischen dem vorhergesagten Mittelwert und dem beobachteten Ergebnis berechnet wird. Wir kamen zu dem Schluss, dass es notwendig ist, den korrekten Punktschätzer, den Median, zu verwenden, um die Verteilung durch eine einzige Zahl zusammenzufassen, was der operationellen Interpretation des absoluten Fehlers entspricht. Dies bringt jedoch einige unangenehme Eigenschaften des MAE mit sich: Es ist grobkörnig, diskontinuierlich und für langsame Bewegungen unbrauchbar.
Bereiten Sie die Bühne für die Rangwahrscheinlichkeitsbewertung vor.
Offensichtlich ist die Situation, die ich Ihnen im ersten Teil dieses Blogbeitrags geschildert habe, nicht zufriedenstellend: Der MAE ist diskontinuierlich, ungenau und sogar nutzlos für langsame Kursbewegungen mit prognostizierten Mittelwerten unter 0,69. Dennoch bleibt die vernünftige betriebswirtschaftliche Interpretation – die Kosten sind proportional zum Fehler – attraktiv. Können wir das reparieren?
Könnten wir den Median einfach weglassen und eine andere Kennzahl verwenden, zum Beispiel den viel aussagekräftigeren Mittelwert? Leider wird die Unterscheidung zwischen Median und Mittelwert nicht dadurch irrelevant, dass man so tut, als sei sie es auch. Dieser Weg löst unsere Probleme nicht, sondern führt zu neuen: Die Vorhersage, die bei einem falsch berechneten MAE zutreffen würde, wäre verzerrt.
Welche Möglichkeiten haben wir also, den AE zu verbessern, wenn wir doch den Median als zusammenfassende Kennzahl verwenden? Einen Aspekt können wir ändern, nämlich die Reihenfolge der beiden Prozesse „Zusammenfassen“ und „Fehler berechnen“. Aktuell fassen wir zuerst die Verteilung zusammen (zugeordnet dem Punktschätzer) und berechnen dann den Fehler („Punktschätzer — Ergebnis“). Lassen Sie uns tief durchatmen und die beiden Schritte vertauschen, wie in der folgenden Grafik (linke Seite) dargestellt: Gegeben eine vorhergesagte Verteilung (rot) und ein beobachtetes Ergebnis (blau), berechnen wir den AE für jedes vorhergesagte Ergebnis (schwarze Pfeile):
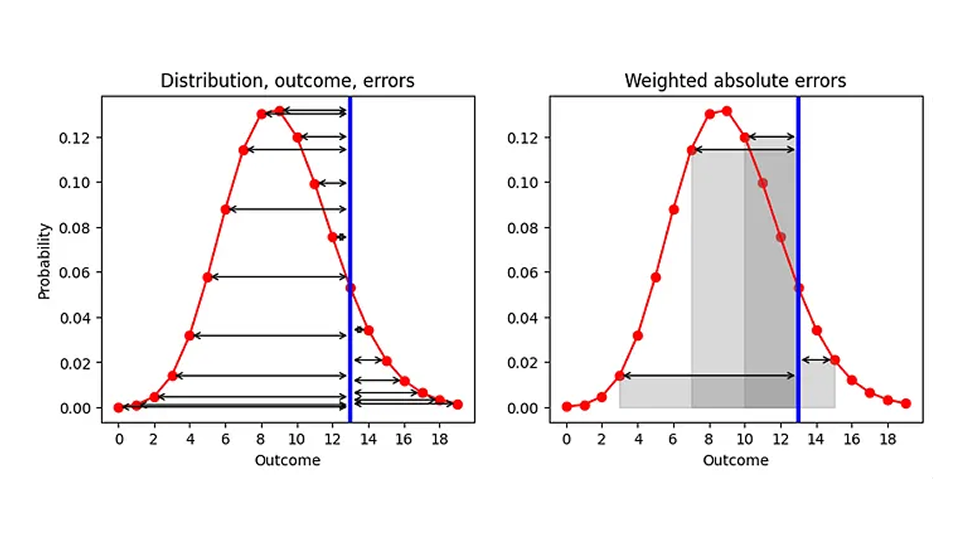
Das Ergebnis ist eine Liste von AEs, eines für jedes Ergebnis (einschließlich der Vorhersage, die mit dem tatsächlichen Ergebnis übereinstimmt, für die AE 0 ist). Da unser Ziel darin besteht, AE durch eine einzelne Zahl zu ersetzen, müssen wir diese vielen AEs zusammenfassen. Nehmen wir den Mittelwert der AEs, wobei die Wahrscheinlichkeit, die wir jedem Ergebnis zugewiesen haben, als Gewicht in diesen Mittelwert einfließt. Geometrisch gesehen addieren wir die Flächen, die von den Fehlerpfeilen und der x-Achse eingeschlossen werden, wie es für einige Ergebnisse in der rechten Grafik dargestellt ist.
Diese Vorschrift stellt eine sinnvolle Definition für den Abstand zwischen einer Zahl und einer Wahrscheinlichkeitsverteilung dar: Man gewichtet jeden Abstand zu einem möglichen Ergebnis mit der diesem Ergebnis zugeordneten Wahrscheinlichkeit. Als Grenzfall, wenn die Verteilung überall 0 wäre, außer bei einem Ergebnis, bei dem sie 1 ist (eine deterministische Vorhersage, die vorhersagt, dass dieses Ergebnis definitiv eintreten wird), erhalten wir den traditionellen AE: Der Absolutwert der Distanz zwischen diesem deterministisch vorhergesagten Ergebnis und der Beobachtung. Unser verbesserter AE wird zum traditionellen AE für deterministische Prognosen!
Wir können das Rezept mit folgender Formel ausdrücken:
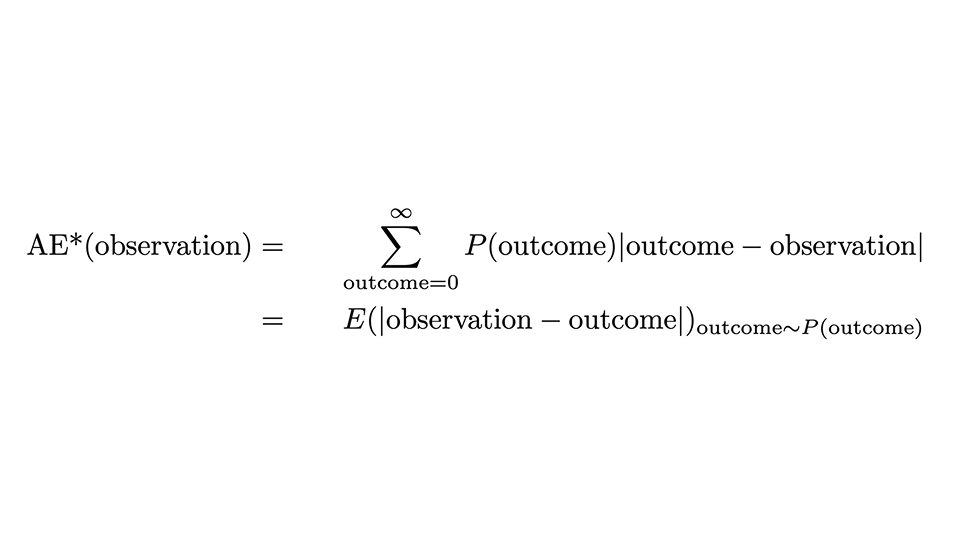
Es sieht zwar etwas beängstigend aus, aber gehen wir es vorsichtig durch: Der AE*, der „korrigierte AE“, für eine Beobachtung ist der AE für diese einzelne Beobachtung, jedoch gemittelt über alle möglichen Ergebnisse (die Summe über das Ergebnis), wobei die vorhergesagte Wahrscheinlichkeit P(Ergebnis) als Gewicht dient. Die zweite Zeile drückt aus, dass dies mit dem Erwartungswert des absoluten Abstands zwischen Beobachtung und Ergebnis übereinstimmt, wenn das Ergebnis gemäß der Wahrscheinlichkeitsverteilung verteilt ist.
Was für eine Fahrt! Wir sind noch nicht ganz so weit, aber fast: Der AE* ist nicht genau der Rangwahrscheinlichkeitswert, und wir haben immer noch keine Ahnung, woher dieser umständliche Name kommt.
Der oben definierte AE* hat eine unerwünschte Eigenschaft: Wenn die wahre Verteilung eine Poisson-Verteilung mit einem bestimmten Mittelwert ist, wird der niedrigste, beste AE* nicht durch Angleichung an diesen Mittelwert erreicht, sondern durch einen etwas kleineren. Wenn Ihre Prognose bei AE* gewinnt, ist sie wahrscheinlich verzerrt und unterschätzt das tatsächliche Ergebnis. Der Grund dafür ist, dass die absolute Breite der Verteilung mit dem Mittelwert zunimmt, was kleinere Mittelwerte begünstigt (und noch einmal eine Gelegenheit, auf die vorherigen Blogbeiträge hinzuweisen [Links zu Forecasting Few is Different 1&2]). Dieses Problem ist lösbar: Wir müssen die Hälfte der erwarteten Breite der Verteilung abziehen, um dies zu berücksichtigen, d. h. den erwarteten Abstand zwischen zwei zufälligen Ergebnissen, die beide aus der vorhergesagten Verteilung stammen. Dies ergibt schließlich den Rangwahrscheinlichkeitswert:
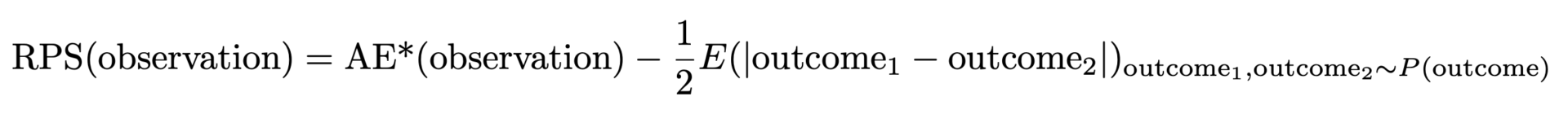
Aber warum heißt diese Methode Ranked Probability Score (RPS), und warum ist sie so unbeliebt? Das RPS wird üblicherweise über abstrakte Formeln eingeführt, die viele Wahrscheinlichkeiten, Stufenfunktionen und kumulative Wahrscheinlichkeiten enthalten. Oft wird sie mit einer rein wahrscheinlichkeitstheoretischen Interpretation präsentiert, was durchaus Sinn ergibt, wenn man sich mit Wahrscheinlichkeitstheorie und Statistik auskennt, für Praktiker jedoch unzugänglich bleibt. Es ist wirklich bemerkenswert, dass die beiden Formulierungen – unsere „verbesserte AE“ und die wahrscheinlichkeitstheoretische – übereinstimmen: Das hässliche Entlein (in den Augen des Anwenders) entpuppt sich als schöner Schwan.
Wie der Rangwahrscheinlichkeitswert die Schwächen des mittleren absoluten Fehlers behebt
Im ersten Teil dieses Beitrags habe ich argumentiert, dass MAE mit unpraktischen Eigenschaften einhergeht: Es ist grobkörnig, diskontinuierlich und für langsame Bewegungen nutzlos. Löst RPS, das „verbesserte MAE“, diese Probleme? In der Tat!
Im folgenden Diagramm wird der RPS (schwarze Linie) mit dem AE (blaue Linie) verglichen, wiederum für eine Beobachtung von 9 (rote gestrichelte Linie). Bei Vorhersagen, die weit vom Ergebnis 9 entfernt sind, verhalten sich RPS und AE ähnlich, wobei RPS nur geringfügig unter AE bleibt. Wenn der vorhergesagte Mittelwert und der beobachtete Wert bei 9 übereinstimmen, erreicht AE den Wert Null, während RPS etwas skeptischer ist: Da RPS die Verteilung kennt, geht es davon aus, dass das exakte Übertreffen des Ergebnisses mit dem Median der vorhergesagten Verteilung auch zufällig sein könnte: Vielleicht lag die tatsächliche Verkaufsrate an diesem Tag bei 7, und wir hatten einfach Glück, dass die beobachtete Nachfrage 9 betrug. Daher erreicht RPS niemals den Wert Null: Kein einzelnes Ergebnis beweist eindeutig, dass eine Wahrscheinlichkeitsvorhersage korrekt war. Bei Abweichungen vom Ergebnis 9 ist AE streng und bestraft Abweichungen sofort mit den entsprechenden Kosten. RPS ist hier wohlwollender und steigt nicht so schnell an wie AE, was widerspiegelt, dass ein „etwas daneben“ auch auf Pech zurückzuführen sein kann und nicht sofort sanktioniert werden muss. Dies entspricht der Geschäftsrealität viel besser: Betriebsabläufe werden oft so geplant, dass geringfügige Abweichungen tolerierbar sind. Alle wünschen sich eine deterministische Prognose, aber niemand erwartet sie ernsthaft, und dafür gibt es Sicherheitsbestände. Sobald die Abweichungen größer werden, verursachen sie reale Kosten.
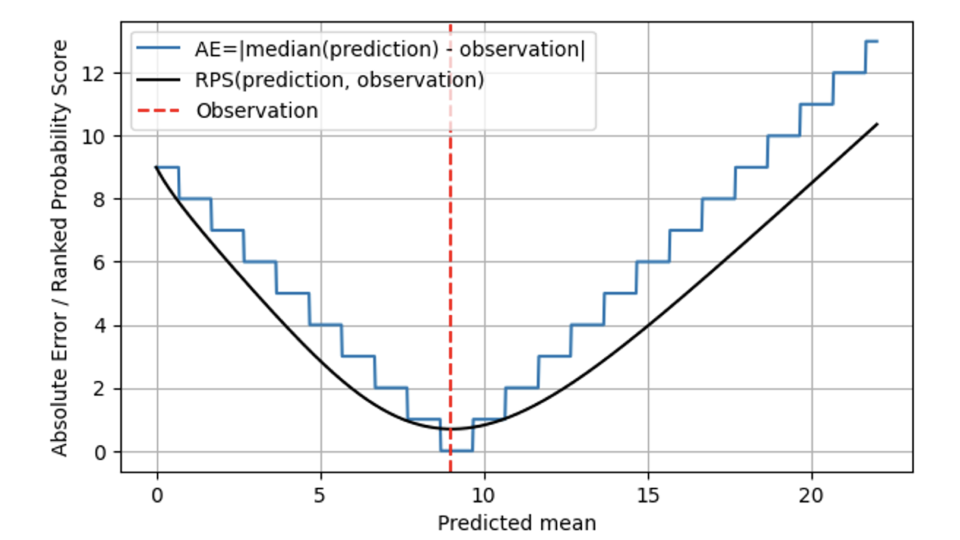
Insgesamt springt der Rangwahrscheinlichkeitswert nicht zwischen verschiedenen Werten hin und her, sondern ist, mathematisch gesprochen, im vorhergesagten Mittelwert stetig . Bei AE sind die Vorhersagen von 8,7, 9,3 und 9,6 nicht zu unterscheiden, bei RPS hingegen schon: Der minimale RPS-Wert wird genau bei einem vorhergesagten Mittelwert von 9 erreicht.
Für Produkte mit geringem Absatzvolumen ist die RPS-Methode hilfreich, aber sie ist kein Allheilmittel: Es wird immer schwierig bleiben, ein Produkt, das sich einmal in 100 Tagen verkauft, von einem zu unterscheiden, das sich einmal in 200 Tagen verkauft, selbst wenn man die RPS-Methode anwendet. Dennoch nimmt RPS selbst bei kleinen Abweichungen der Vorhersagen, wie beispielsweise 0,6, 0,06 und 0,006, unterschiedliche Werte an.
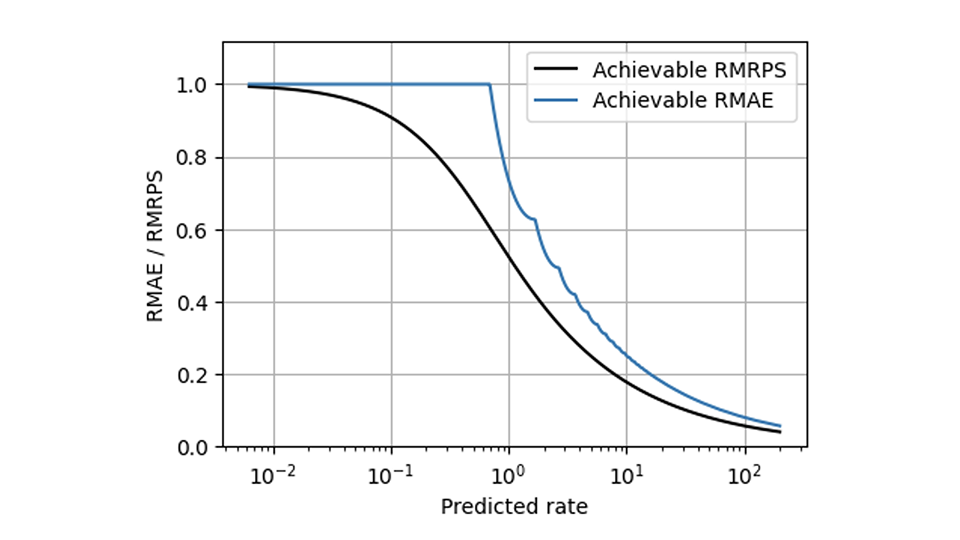
RPS hilft bei vielen Problemen von MAE, aber es gibt eine Herausforderung, die selbst RPS nicht lösen kann: Die unvermeidliche Skalierung, die dazu führt, dass sich langsam und schnell verkaufende Produkte unterschiedlich verhalten. Die Methoden, die Metriken skalierungsfähig machen (teilweise in diesem Blog beschrieben [Links zu Forecasting Few is different 1&2]), können jedoch auf RPS in der gleichen Weise angewendet werden, wie sie auf AE angewendet wurden. Im Vergleich zum relativen MAE weist der relative mittlere RPS (der mittlere RPS geteilt durch die mittlere Beobachtung) in dieser Grafik eine deutlich gleichmäßigere Form auf und zeigt den bestmöglichen Wert für beide Metriken:
Wann sollte man MRPS anstelle von MAE verwenden?
Aussagekräftige Prognosen sind niemals deterministisch und sicher, sondern immer probabilistisch und unsicher, was bei der Bewertung berücksichtigt werden muss. Zu sagen, dass Menschen Unsicherheit nicht mögen, ist eine gewaltige Untertreibung: Menschen hassen Unsicherheit. Menschen sind bereit, viel erwarteten Nutzen zu opfern, um vollkommene Gewissheit zu erlangen (was, wenn das Risiko tödlich ist, durchaus vernünftig ist). Wenn Geschäftsverantwortlichen mitgeteilt wird, dass eine Prognose „nur“ eine Wahrscheinlichkeitsvorhersage liefert, wünschen sie sich oft stattdessen eine deterministische Vorhersage, und die Prognostiker müssen sie enttäuschen, indem sie sich weigern, eine solche zu erstellen. Unvermeidbare Unsicherheiten explizit zu benennen, ist jedoch kein Zeichen von Schwäche, sondern von Vertrauenswürdigkeit.
Die gesamte Ausdruckskraft einer Wahrscheinlichkeitsverteilung, die die Wahrscheinlichkeit jedes denkbaren Ergebnisses enthält, auf eine einzige Zahl zu reduzieren, ist so simplistisch, grobkörnig und ungenau, wie es scheint – obwohl man dies in der Praxis tun muss, wenn man Artikel einlagert. Aus konzeptioneller Sicht liefert der Rangwahrscheinlichkeitswert daher eine wesentlich bessere Antwort auf die Frage „Wie weit liegt das Ergebnis von der Vorhersage entfernt?“ als der absolute Fehler.
Wenn der Wahrscheinlichkeitscharakter der Prognose irrelevant ist, wird der Unterschied zwischen AE und RPS vernachlässigbar, und AE und RPS können austauschbar verwendet werden (wobei erstere einfacher zu berechnen ist als letztere, wobei letztere etwas kleinere Werte voraussetzt). Das heißt, wenn die Breite der Wahrscheinlichkeitsverteilung viel kleiner ist als die typischen Fehler, die auftreten, kann ich als Prognostiker auftretende Fehler nicht auf „unvermeidbares Rauschen, gegen das man nichts tun kann“ zurückführen. Wenn ich beispielsweise für bestimmte Artikel eine Verkaufsprognose von 1000 Stück abgebe und nicht besonders ehrgeizig bin und mich schon mit Ergebnissen zwischen 800 und 1200 zufrieden geben würde, wird der Unterschied zwischen der Verwendung von RPS und AE marginal. Der Einfachheit halber sollte ich dann bei AE bleiben.
Immer wenn wir uns im Bereich der mittleren bis langsamen Bewegungen bewegen, also wenn wir Mittelwerte wie 0,8, 7,2 oder 16,8 prognostizieren, macht es einen Unterschied, ob wir die Verteilung auf eine einzige Zahl reduzieren, um AE zu bewerten, oder ob wir den etwas komplexeren Weg mit RPS wählen. Wenn wir „1“ vorhersagen, meinen wir damit, dass die Wahrscheinlichkeit, „1“ zu beobachten, bei etwa 37 % liegt, genauso wie die Wahrscheinlichkeit, „0“ zu beobachten. Die Wahrscheinlichkeitsnatur von Prognosen im mittleren bis langsamen Verkaufsbereich zu vernachlässigen, ist daher gefährlich und irreführend. Aber jetzt wissen Sie, wie Sie die Wahrscheinlichkeitsverteilung berücksichtigen: Mithilfe des Rangwahrscheinlichkeitswerts, den Sie hoffentlich jetzt auch als den schönen Schwan unter den Prognosebewertungsmethoden sehen, der sowohl Statistiker als auch Praktiker zufriedenstellt.













