Der mittlere absolute Fehler ist für Praktiker die erste Wahl, wenn es um die Bewertung ihres Modells geht, da er einfach definiert ist und eine intuitive geschäftliche Relevanz besitzt. Die Bewertungsmetrik Ranked Probability Score ist hingegen auf den ersten Blick keine besonders ansprechende Funktion: Ihr abschreckender Name passt gut zu ihrer umständlichen formalen Definition, was erklärt, warum fast kein Praktiker im Bereich Supply Chain Management sie kennt, geschweige denn anwendet. Aber sie verpassen etwas! Der Rangwahrscheinlichkeitswert ist die natürliche Erweiterung des mittleren absoluten Fehlers auf den Bereich der probabilistischen Prognosen, d. h. auf Prognosen, die ihre eigene Unsicherheit „kennen“. Es beinhaltet eine intuitive Interpretation und löst mehrere der gravierenden Probleme des mittleren absoluten Fehlers. Der Rangwahrscheinlichkeitswert spiegelt die Geschäftslage noch besser wider als der mittlere absolute Fehler und berücksichtigt statistische Unsicherheiten, wodurch die theoretische statistische Theorie mit der alltäglichen Praxis in Einklang gebracht wird.
Ein plausibler Geschäftsstandard: Mittlerer absoluter Fehler
„Welche Kennzahl sollen wir zur Bewertung des Nachfrageprognosemodells verwenden?“
Diese Frage wird üblicherweise mit dem „mittleren absoluten Fehler“ beantwortet, und das aus durchaus soliden Gründen. Der absolute Fehler (AE) spiegelt oft angemessen die Kosten einer fehlerhaften Prognose wider: Wenn ich beispielsweise den Verkauf von 8 Körben Erdbeeren prognostiziere und 8 Körbe einlagere, die tatsächliche Nachfrage aber 9 beträgt, ergibt sich ein AE von 1, und ein unzufriedener Kunde wendet sich an die Konkurrenz. Wenn meine Prognose 11 Körbe bei gleicher Nachfrage von 9 lautet, beträgt der absolute Fehler 2, und ich habe 2 Körbe Erdbeeren zu entsorgen. Für das beobachtete Ergebnis 9 wird der AE in der folgenden Grafik als Funktion der Vorhersage durch die blaue Linie dargestellt:
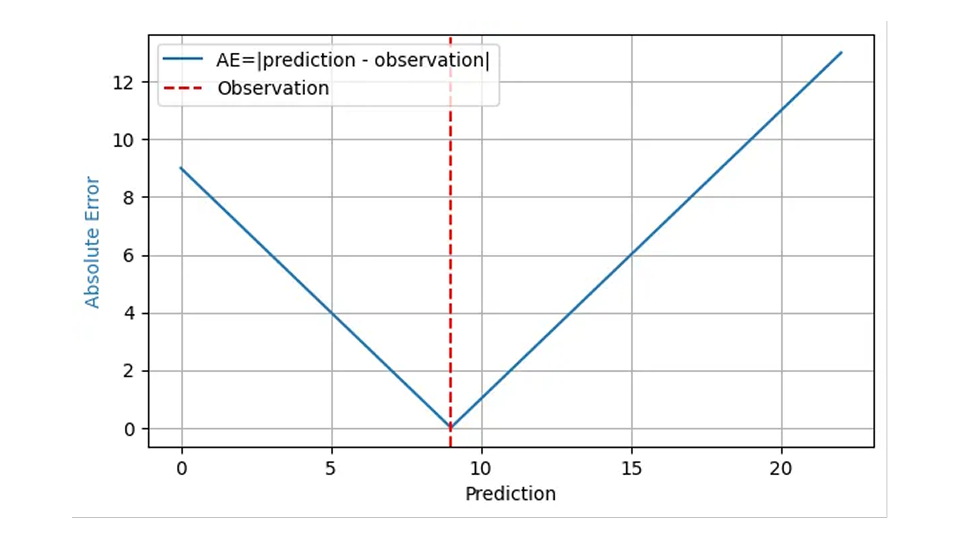
Da die finanziellen Auswirkungen eines Prognosefehlers typischerweise proportional zum Prognosefehler selbst sind, spiegelt der Mittelwert des absoluten Fehlers (AE) über viele Vorhersagen und Ergebnisse hinweg, der mittlere absolute Fehler (MAE), die Geschäftskosten wider, zumindest unter der Annahme, dass ein Überbestand die gleichen finanziellen Auswirkungen hat wie ein Unterbestand. Der mittlere quadratische Fehler (MSE) würde bedeuten, dass eine Abweichung von „eins“ umso kostspieliger wird, je größer der Fehler bereits ist – was in der Geschäftswelt ziemlich unrealistisch ist. Der mittlere absolute prozentuale Fehler (MAPE), der Mittelwert des normalisierten absoluten Fehlers, Mittelwert (absoluter Fehler/beobachtetes Ergebnis), ist mit ernsthaften unerwarteten Fallstricken behaftet (wie in diesem früheren Blogbeitrag beschrieben) und kann für die Bedarfsprognose getrost verworfen werden.
Daher ist es für Praktiker ratsam, MAE oder dessen normalisierte Variante Relative MAE, RMAE = MAE / Mittelwert(Ergebnis), als erste einfache Wahl zur Bewertung ihrer Modelle zu verwenden. Die typischen Werte für MAE und RMAE sind jedoch skalenabhängig: Die Prognose für Milchflaschen (Schnellverkäufer) wird naturgemäß einen höheren MAE-Wert und einen niedrigeren RMAE-Wert aufweisen als die Prognose für bestimmte Spezialbatterien (Langsamverkäufer). Das ist zugegebenermaßen nicht leicht zu erkennen, weshalb der Blogbeitrag zu diesem Thema nicht einmal einen einzigen Beitrag füllte, sondern in "Forecasting few is different part 1" und "part 2" aufgeteilt wurde.
Da MAE einfach, bekannt und relevant ist, warum sollte man einen Blogbeitrag über eine Alternative schreiben oder lesen? Sich blind auf eine Bewertungsmetrik zu verlassen, ist sicherlich eine der unwissenschaftlichsten Vorgehensweisen im Hinblick auf Datenanalyse. Lasst uns MAE gründlich unter die Lupe nehmen, um zu sehen, ob es sich wirklich so verhält, wie wir es erwarten, und wenn nicht, wie wir das Problem beheben können. Um es kurz zu machen: Bei der Bewertung von AE werden Sie auf einige unerwartete, unangenehme Komplikationen stoßen, die jedoch durch eine verwandte, aber oft unterschätzte Kennzahl, den Rangwahrscheinlichkeitswert, sanft gelöst werden.
Moment, nicht so schnell! Wie man den mittleren absoluten Fehler für Wahrscheinlichkeitsprognosen bewertet
Bislang haben wir so getan, als sei „eine Prognose“ einfach eine Zahl, genau wie das prognostizierte Ziel selbst (die Anzahl der verkauften Artikel, zum Beispiel die Anzahl der Erdbeerkörbe, Äpfel, Milchflaschen oder roten T-Shirts). Die Berechnung der Differenz zwischen einer solchen Prognose (einer Zahl) und der tatsächlichen Beobachtung (einer anderen Zahl) ist dann überhaupt kein Problem: Ich sage voraus, dass 10 Äpfel verkauft werden, es wurden 7 verkauft, der absolute Fehler beträgt 3. Kein Doktortitel in Statistik erforderlich.
Aber es gibt einen kleinen Unterschied: Was wäre, wenn ich vorhergesagt hätte, dass 10,4 statt 10 Äpfel verkauft werden? Wie hätte ich mich hinsichtlich der Lagerhaltung entschieden? Vermutlich hätte ich trotzdem 10 Äpfel bestellt, das heißt, der geringe Unterschied von 0,4 in der Prognose hätte operativ keinen Unterschied gemacht, das Geschäftsergebnis wäre dasselbe gewesen. Dennoch wäre der absolute Fehler etwas größer, nämlich 3,4 statt 3. Der gleichmäßige Verlauf des absoluten Fehlers in der Vorhersage in der ersten Abbildung ist irreführend: Die Differenz zwischen Vorhersage und Istwert ist nicht die für das Unternehmen relevante Größe, sondern die Differenz zwischen der Anzahl der bestellten Artikel und der tatsächlichen Anzahl. Warum sollte ich dann jemals etwas anderes als eine ganze Zahl vorhersagen, wenn ich doch weiß, dass nur ganzzahlige Größen auftreten können?
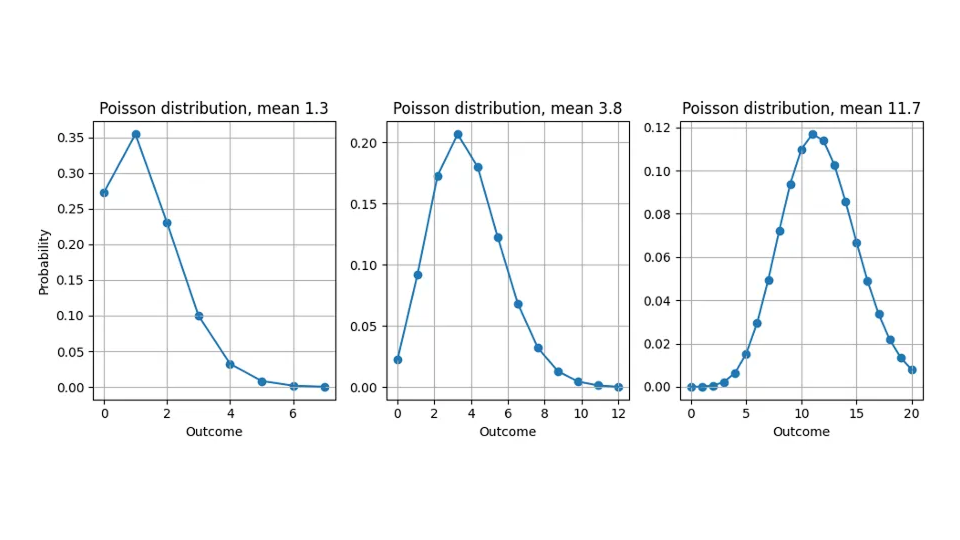
Der Grund für diese Diskrepanz – wir prognostizieren nicht-ganzzahlige Werte, messen aber nur ganzzahlige Größen – liegt darin, dass die meisten Prognosen keine „Punktprognosen“ sind, die eine universelle, bewertungsunabhängige „beste Schätzung“ für das Ziel ausdrücken, sondern eine Wahrscheinlichkeitsverteilung liefern (keine Sorge: ein Doktortitel in Statistik ist immer noch nicht erforderlich). Sie geben uns an, wie wahrscheinlich jedes mögliche Ergebnis ist: Wenn wir 10,4 vorhersagen, gehen wir nicht davon aus, dass ein Kunde einen Apfel in Stücke schneidet, um 0,4 davon zu kaufen, sondern wir halten die möglichen Ergebnisse „11“, „12“, „13“ für wahrscheinlicher als bei einer Vorhersage von 10,0. Prognosen sind daher nicht nur Zahlen, die mit dem Zielwert verglichen werden können, sondern Funktionen. Auch wenn die Diskussion auf jede beliebige Verteilung anwendbar ist, gehe ich in diesem Blogbeitrag davon aus, dass die vorhergesagte Wahrscheinlichkeitsverteilung die Poisson-Verteilung ist (siehe dazu unsere verwandten Blogbeiträge hier und hier).
Hier sehen Sie, welche Wahrscheinlichkeitsverteilung wir implizit annehmen, wenn wir 1,3, 3,8 oder 11,7 vorhersagen:
Zurück zur Berechnung des absoluten Fehlers: Wie können wir eine Funktion von einer Zahl subtrahieren? Es macht keinen Sinn, 7 verkaufte Artikel von einer Wahrscheinlichkeitsverteilung abzuziehen. Wir müssen die vorhergesagte Wahrscheinlichkeitsverteilung durch eine einzige Zahl zusammenfassen , um einen Vergleich zu ermöglichen. Diese zusammenfassende Zahl wird als Punktschätzer bezeichnet und kann dann vom beobachteten tatsächlichen Wert subtrahiert werden, um den Fehler zu erhalten.
Wahrscheinlichkeitsverteilungen können auf viele Arten zusammengefasst werden: Der Mittelwert ist die unmittelbarste, aber Verteilungen können auch durch ihr wahrscheinlichstes Ergebnis (ihren Modus), durch das Ergebnis, das die Wahrscheinlichkeitsverteilung in zwei gleiche Hälften teilt (ihren Median), oder durch andere Vorgaben zusammengefasst werden.
In diesem Zoo von Punktschätzern fühlen sich manche natürlicher an als andere – können wir einfach die Zusammenfassung auswählen, die uns am besten gefällt? Nein, der korrekte Punktschätzer wird durch die gewählte Bewertungsmetrik festgelegt. Mit anderen Worten: Sie können wählen, welche Fehlermetrik meine Prognose bewertet (MAE, MAPE, MSE …), aber ich bestimme dann, wie die Prognose für diese Bewertung zusammengefasst wird. Meine Punkteschätzung für einen Sieg bei MAE wird sich von der für einen Sieg bei MSE unterscheiden, geschweige denn von der für einen Sieg bei MAPE. Diese Wahl mag Ihnen willkürlich, vielleicht sogar unehrlich erscheinen, aber sie spiegelt die immense Ausdruckskraft probabilistischer Prognosen wider: Sie enthalten viel mehr Informationen als nur eine einzige „beste Vermutung“. Je nachdem, wie sie bewertet werden und wie „am besten“ anhand der Fehlermetrik tatsächlich definiert wird, wird der Wert, der bei einer bestimmten Bewertungsmethode den Ausschlag gibt, entsprechend ausgewählt. Anders ausgedrückt: Die Aufforderung „Geben Sie mir Ihre beste Prognose“ ist bedeutungslos, solange nicht klar ist, wie „beste“ definiert wird. Eine einzelne Wahrscheinlichkeitsprognose kann viele verschiedene Punktschätzer oder „beste Schätzungen“ erzeugen, je nachdem, wie die Prognose bewertet wird.
Bei der Berechnung des quadratischen Fehlers (SE) entspricht der Punktschätzer dem Mittelwert der Verteilung. Bei der Berechnung des absoluten prozentualen Fehlers (APE) handelt es sich um einen Punktschätzer, der eine wirklich kontraintuitive Funktion darstellt, mit der ich Sie nicht belästigen werde, was zu unerwarteten Paradoxien bei der MAPE-Berechnung führt.
Der absolute Fehler erfordert den Median der Verteilung, nicht den Mittelwert, und ja, das ist wichtig.
Für den absoluten Fehler (AE) ist der Median der korrekte Punktschätzer. Ja, der Median, nicht der Mittelwert, und nein, wir können nicht einfach den Mittelwert verwenden. Ich möchte Ihnen erklären, warum nur der Median für AE optimal sein kann. Nehmen wir eine Prognose, also eine Verteilung, und zwar die Poisson-Verteilung mit Mittelwert 3,8 und Median 4. Wie viele Artikel würden Sie bei dieser Prognose einlagern? Das Ergebnis muss eine ganze Zahl sein, es kann nicht 3,8 sein. Um die richtige Lagermenge zu ermitteln, wählen wir die Schätzung so, dass der AE, den wir im Durchschnitt bei der Beobachtung von Ergebnissen aus dieser Verteilung finden, so klein wie möglich ist.
Wir suchen nach dem richtigen Punktschätzer, der diese gesamte Verteilung in eine einzige Zahl zusammenfasst, die operativ beste Lagermenge. In dieser Abbildung probiere ich drei verschiedene Schätzungen aus (3, 4, 5):
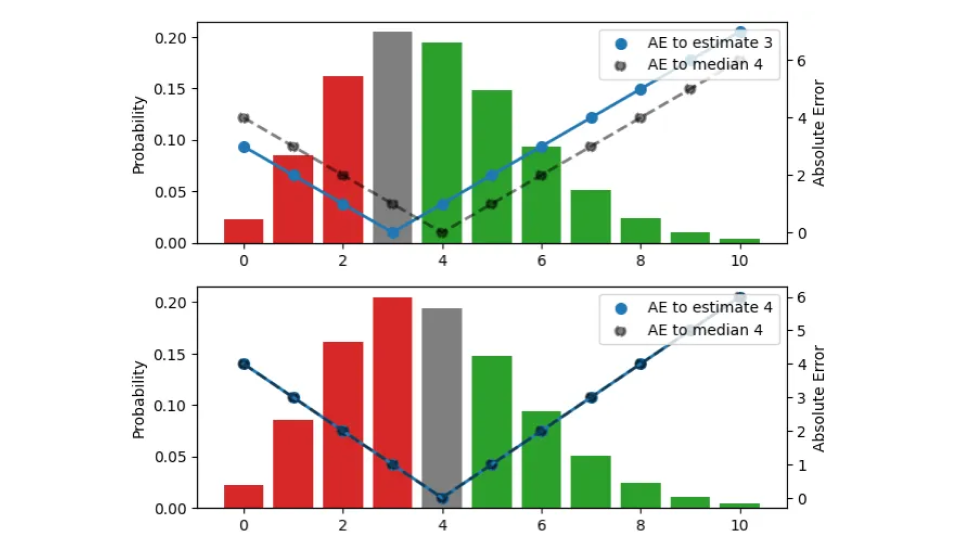

Die Wahrscheinlichkeitsverteilung, visualisiert durch die Balken (linke Skala), ist in allen drei Diagrammen gleich. Im oberen Feld wird die Schätzung 3 dargestellt, im mittleren Feld ist es die Schätzung 4, im unteren Feld ist es die Schätzung 5. Die absolute Abweichung (AE) zwischen Schätzung und Ergebnissen wird durch die blauen Punkte dargestellt, die durch die durchgezogene Linie verbunden sind (rechte Skala). Die absolute Abweichung (AE) in Bezug auf den Median 4 wird durch schwarze Punkte dargestellt, die durch eine gestrichelte Linie verbunden sind. Wenn beispielsweise der Schätzwert 3 beträgt (oberes Diagramm), verschwindet der Fehler für das Ergebnis 3, und die blaue durchgezogene Linie trifft auf 0. Bei einem Beobachtungswert von 4 oder 2 beträgt der Fehler 1.
Die Farbe der Balken gibt an, ob ein vorhergesagtes Ergebnis zum absoluten Fehler beiträgt, weil es kleiner (rot) oder größer (grün) als die Schätzung ist; die Balkenhöhe entspricht der Wahrscheinlichkeit, dass es eintritt. Wenn ein Ergebnis mit der Schätzung übereinstimmt, trägt es nichts zum Fehler bei und wird grau dargestellt. Durch die Verschiebung der Schätzung um eine Einheit nach oben bewegen wir uns um ein Feld nach unten. Alle Beobachtungen unter den roten Balken und unter dem grauen Balken tragen zu einer zusätzlichen Fehlereinheit für die neue, verschobene Schätzung bei: Bei der vorherigen Schätzung 3 hatte das Ergebnis 2 einen Fehler von 1, bei der Schätzung 4 hat dasselbe Ergebnis einen Fehler von 2. Umgekehrt tragen alle Beobachtungen, die zuvor grüne Balken hatten, nach der Verschiebung zu einer um eine Fehlereinheit geringeren bei: Bei der Schätzung 3 hatte das Ergebnis 5 einen Fehler von 2, bei der Schätzung 4 sinkt der Fehler auf 1.
Fassen wir zusammen, was passiert, wenn der Schätzwert um eine Einheit erhöht wird: Der Erwartungswert von AE unter der Verteilung steigt für diejenigen Ergebnisse, die kleiner oder gleich dem Schätzwert sind (wir überschätzen sie noch stärker als zuvor) und sinkt für diejenigen, die größer als der Schätzwert sind (wir unterschätzen sie weniger stark). Die Zunahme ist proportional zur Gesamtfläche der roten und grauen Balken, die Abnahme ist proportional zur Fläche der grünen Balken.
In voller Analogie dazu trägt bei einer Verringerung der Schätzung um eine Einheit jede Beobachtung unter den grünen Balken oder unter dem grauen Balken zu einer weiteren Fehlereinheit bei, und alle Beobachtungen in den roten Balken tragen zu einer geringeren Fehlereinheit bei.
Bei einer gegebenen Verteilung führt eine Verschiebung des Schätzwertes um eins nach oben oder unten zu einer Erhöhung bzw. Verringerung des resultierenden erwarteten absoluten Fehlers. Den richtigen Schätzwert finden wir, indem wir nach dem Minimum suchen. Vielleicht haben Sie diese Faustregel schon einmal aufgestellt: Wenn die meisten Ergebnisse für die aktuelle Schätzung zu niedrig ausfallen, verringern Sie die Schätzung; wenn die meisten Ergebnisse zu hoch ausfallen, erhöhen Sie sie. Nur wenn die Differenz zwischen den Wahrscheinlichkeitsmassen, die mit Über- und Untervorhersagen zusammenhängen (die Differenz zwischen den Gesamtflächen der „roten“ und „grünen“ Balken), kleiner ist als der graue Balken, kann der Fehler nicht weiter verbessert werden. Dies ist im mittleren Feld der Fall: Die Schätzung ist so beschaffen, dass die Wahrscheinlichkeitsmassen darunter und darüber nahezu übereinstimmen, sodass eine Bewegung in die eine oder andere Richtung den Gesamtfehler erhöhen würde. Diese Schätzung entspricht dem Median: Wenn Ihnen eine Wahrscheinlichkeitsverteilung gegeben ist, ist der Punktschätzer, der den absoluten Fehler minimiert, in der Hälfte der Fälle höher oder niedriger als die Ergebnisse.
Ich halte es für wichtig, diesen Punkt hervorzuheben, da er oft unberücksichtigt bleibt: Wenn 7,3 die beste Schätzung für den Mittelwert einer Verteilung ist, besteht die korrekte Methode zur Bestimmung des absoluten Fehlers bei einer Beobachtung von beispielsweise 9 nicht darin, 7,3 von 9 zu subtrahieren, sondern den Median dieser Verteilung (bei der Poisson-Verteilung 7) von 9 zu subtrahieren. Praktisch gesehen ist 7 genau die Anzahl der Artikel, die man bei einer Vorhersage von 7,3 einlagern würde. Überraschenderweise hilft es Ihnen nicht, eine genaue Schätzung des Mittelwerts für Aktienentscheidungen zu haben; es spielt keine Rolle, ob die Prognose 7,1 oder 7,3 lautet: Sie müssen sich für eine ganze Zahl entscheiden. Bei der Aggregation von Prognosen auf einer höheren Ebene für die Planung wird die Unterscheidung zwischen 7.1 und 7.3 jedoch wichtig.
Diese Unterscheidung zwischen Mittelwert und Median mag Ihnen wie Haarspalterei vorkommen: Schließlich scheinen der Wert, der die Wahrscheinlichkeit in zwei gleiche Hälften teilt, und der Mittelwert dieser Verteilung sehr ähnlich zu sein, und sie liegen bei den meisten wohlwollenden Verteilungen (wie der Poisson-Verteilung, die für den Einzelhandel relevant ist) nahe beieinander. Allerdings können zwei Verteilungen denselben Mittelwert, aber unterschiedliche Mediane haben; zwei andere Verteilungen können im Median übereinstimmen, sich aber im Mittelwert unterscheiden. Die Begriffe Mittelwert und Median einfach synonym zu verwenden, würde Sie daran hindern, die beste Prognose zu finden.
Die unerwarteten Schwächen des mittleren absoluten Fehlers
Wir wissen nun, wie man den absoluten Fehler für Wahrscheinlichkeitsprognosen ermittelt: Wir fassen die Verteilung durch den Median des Punktschätzers (die Anzahl der Artikel, die wir einlagern würden) zusammen, subtrahieren diesen Median vom beobachteten Ergebnis und bilden den Absolutwert. Ich habe versucht, dies in der folgenden Grafik zu visualisieren:
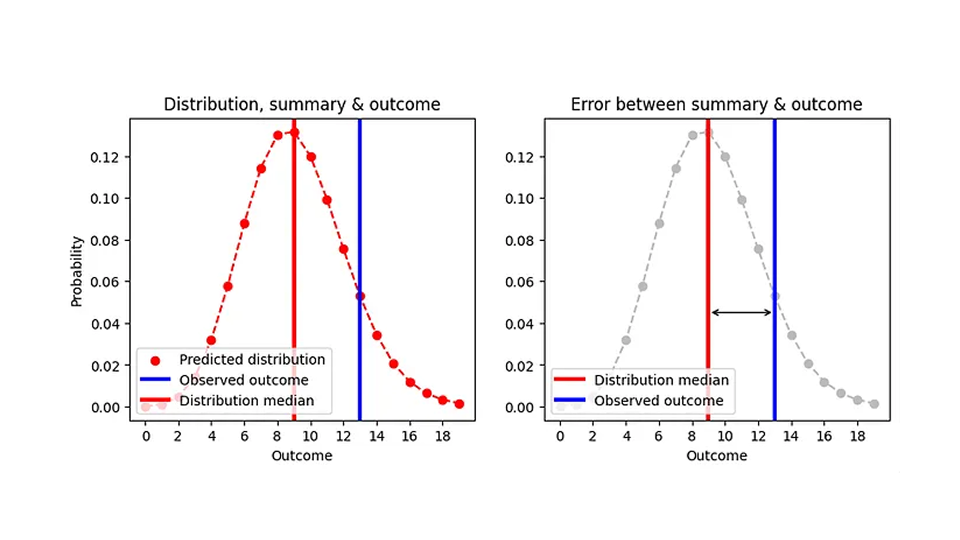
Da der Median immer eine ganze Zahl ist, können zwei völlig unterschiedliche Verteilungen denselben absoluten Fehler ergeben. Beispielsweise ist der AE-Wert für eine Poisson-Prognose von 8,7 (Median=9) und für eine Poisson-Prognose von 9,6 (Median=9) gleich, obwohl sich die Prognosen deutlich unterscheiden, wie wir in dieser Abbildung sehen können:
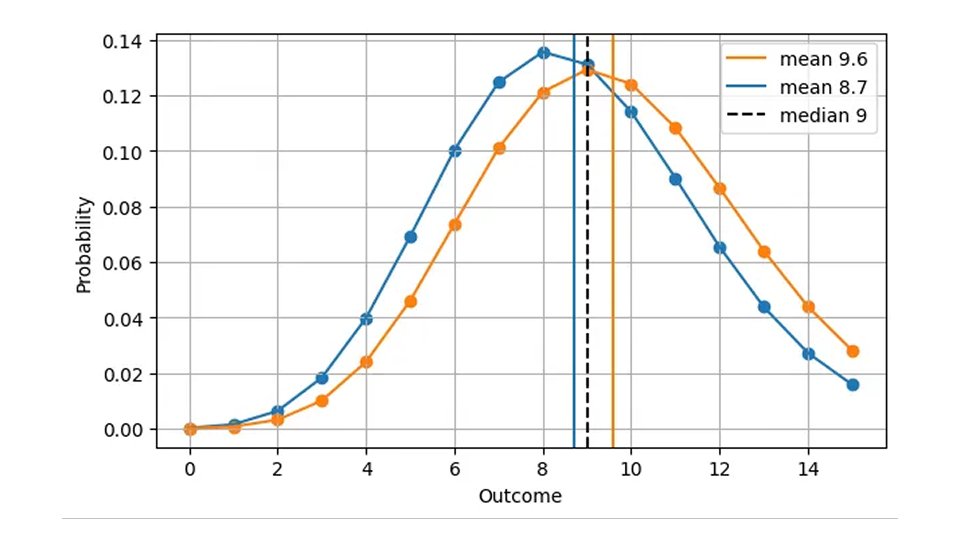
Aus betrieblicher Sicht ist dies sinnvoll: In beiden Fällen ist es richtig, an einem bestimmten Tag 9 Artikel auf Lager zu haben. Folglich ergibt sich für eine realistischere Darstellung der ersten Abbildung, AE als Funktion der Vorhersage, folgendes Bild.
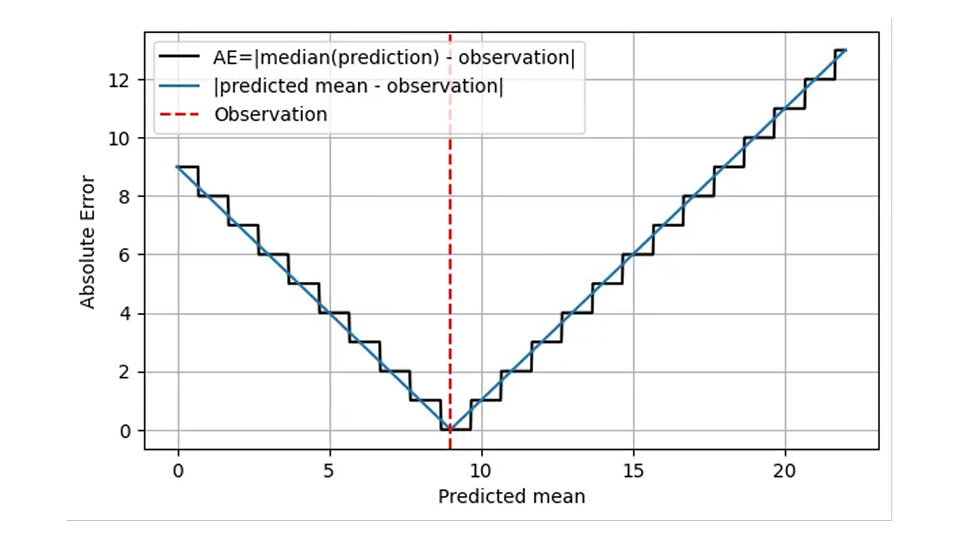
Der AE wird anhand des Medians der Vorhersage (schwarze Linie) berechnet und setzt nur ganzzahlige Werte voraus. Ich möchte etwas genauer erläutern, was die x-Achse bedeutet: Es handelt sich nicht nur um die „Vorhersage“, sondern um den vorhergesagten Mittelwert.
Diese treppenförmige Struktur deutet darauf hin, dass AE grobkörnig und ungenau ist: Wir können die Verteilungen mit Mittelwert 8,7 und 9,6 mit bloßem Auge unterscheiden, AE jedoch nicht! Der MAE allein hilft nicht mehr, die Genauigkeit einer Prognose über einen bestimmten Schwellenwert hinaus zu verbessern, der bei sich langsam bewegenden Artikeln recht dramatisch ist: Der relative Unterschied zwischen 1,7 und 2,6 beträgt 53 %, während der AE einer Prognose von 1,7 und der einer Prognose von 2,6 gleich ist! Dieses grobkörnige Verhalten geht mit unangenehmen Sprüngen und Diskontinuitäten an den Stellen einher, an denen der Median der Verteilung von einem ganzzahligen Wert zum nächsten springt. Operativ macht es keinen Unterschied, ob man für einen bestimmten Tag, Ort und Artikel 1,7 oder 2,6 prognostiziert: Die richtige Menge zum Einlagern beträgt 2. Prognosen werden jedoch auch auf höheren Aggregationsebenen für die Planung verwendet. Auf einem so hohen Niveau bemerkt man tatsächlich den Unterschied zwischen 1,7 und 2,6: Für die nächsten 100 Tage macht es einen großen Unterschied, ob man 170 oder 260 Artikel beim Lieferanten bestellt.
Wenn der prognostizierte Mittelwert unter etwa 0,69 pro Prognosezeitraum liegt (ein langsam verkaufendes Produkt), ist die Prognose mit dem besten absoluten Fehler 0. Erstaunlicherweise haben wir denselben absoluten Fehler für eine Prognose von 0,6, von 0,06 und 0,006, obwohl wir zwei Größenordnungen durchlaufen haben! Die Vorhersage 0 ist in der Lieferkette ziemlich nutzlos, da man in einen Teufelskreis perfekter 0-Vorhersagen gerät: Man lagert 0 ein, man verkauft 0, und die zuvor prognostizierte 0 hat sich selbst erfüllt.













