Dies ist eine zweiteilige Geschichte über den Umgang mit Absatzprognosen für schnell- und langsamdrehende Artikel. Teil 1 finden Sie hier.
Wie präzise kann eine Absatzprognose werden?
Der Mechanismus der Fluktuationskompensation sorgt dafür, dass granulare Vorhersagen im niedrigen Maßstab ungenauer, verrauschter und unsicherer sind als aggregierte, grobkörnige Vorhersagen im hohen Maßstab: Wir sind (relativ gesehen) besser darin, die Gesamtzahl der Brezeln für eine ganze Woche vorherzusagen als für einen einzelnen Tag.
Bislang haben wir diese Beziehung qualitativ begründet, aber können wir eine quantitative Aussage über den Grad an Präzision treffen, den wir idealerweise für verschiedene prognostizierte Verkaufsraten erwarten können? Zum Glück ist dies tatsächlich möglich, und zwar auf eine universelle, branchenunabhängige Weise. In unserem vorherigen Blogbeitrag über den Rückschaufehler bei der Prognosebewertung argumentierten wir, dass deterministische, vollkommen sichere Prognosen unrealistisch sind: Betrachten wir unsere obige Prognose von 5 Brezeln. Auf der Ebene einzelner Kunden bedeutet eine deterministische Prognose von 5, dass 5 Kunden am prognostizierten Tag auf jeden Fall eine Brezel kaufen werden. Wir gehen aber nicht nur davon aus, diese fünf Kunden extrem gut zu kennen (vielleicht besser, als sie sich selbst kennen – wer hat nicht schon einmal spontan entschieden, sich eine Brezel zu schnappen oder nicht?), sondern wir schließen auch völlig aus, dass irgendein anderer Kunde eine Brezel kaufen würde. Ein solcher Grad an Gewissheit ist eindeutig unmöglich. Berücksichtigt man eine gewisse Unsicherheit, beispielsweise 6 Kunden mit einer Wahrscheinlichkeit von jeweils 5/6 = 83,3 %, eine Brezel zu kaufen, ergibt sich eine sogenannte Binomialverteilung in der Gesamtzahl der verkauften Brezeln: Die Wahrscheinlichkeit, 6 Brezeln zu verkaufen, beträgt (5/6)^6, die Wahrscheinlichkeit, keine zu verkaufen, beträgt (1/6)^6, und die Wahrscheinlichkeit, zwischen einer und fünf Brezeln zu verkaufen, enthält die jeweiligen Binomialkoeffizienten. Allerdings ist es unrealistisch, 6 Kunden zu kennen, die mit hoher Wahrscheinlichkeit kaufen werden. Selbst die Annahme, dass 10 Kunden mit jeweils 50%iger Wahrscheinlichkeit eine Brezel kaufen, ist eine Herausforderung. Wir können fortfahren und die Zahl potenzieller Kunden weiter erhöhen, während wir gleichzeitig die Wahrscheinlichkeit verringern, dass sie eine Brezel kaufen, indem wir dem Pfad zur Grenz- Poisson-Verteilung folgen: Im Poisson-Grenzfall gehen wir von einer unbegrenzten Kundenbasis aus, in der jeder Kunde eine infinitesimal kleine Wahrscheinlichkeit hat zu kaufen, während wir die Kontrolle über das Produkt aus der Anzahl der Kunden und der Kaufwahrscheinlichkeit haben: die Verkaufsrate. Die Poisson-Verteilung skaliert konsistent: Wenn die täglichen Umsätze einer Poisson-Verteilung mit einem Mittelwert von 5 folgen, dann folgen die wöchentlichen Umsätze einer Poisson-Verteilung mit einem Mittelwert von 35. Die Poisson-Verteilung ist der „Goldstandard“ für Absatzprognosen: Wir gehen davon aus, alle Faktoren zu kennen, die den Absatz eines bestimmten Produkts beeinflussen, haben aber keinen Zugriff auf individuelle Kundendaten, die es uns ermöglichen würden, stärkere Aussagen über das Kaufverhalten einzelner Kunden zu treffen. Wenn die Genauigkeit Ihrer Prognose so gut ist, wie es die Poisson-Verteilung erwarten lässt, haben Sie in der Regel die Grenze des Machbaren erreicht.
Eine Poisson-Verteilung benötigt nur einen einzigen Parameter, die Verkaufsrate; die Verteilungsbreite, also die Streuung der wahrscheinlichen Ergebnisse um den Mittelwert, wird vollständig durch ihre funktionale Form bestimmt, welche die Selbstkonsistenz widerspiegelt. Das heißt, der erreichbare Genauigkeitsgrad hängt nur von der prognostizierten Verkaufsrate innerhalb des betrachteten Zeitintervalls ab: Der Absatz von 5 prognostizierten Brezeln pro Tag folgt der gleichen Verteilung wie der Absatz von 5 prognostizierten Geburtstagstorten pro Woche, 5 prognostizierten Brötchen pro Stunde oder 5 prognostizierten Hochzeitstorten pro Quartal. Anders ausgedrückt: Der im besten Fall erreichbare relative Fehler wird vollständig und eindeutig durch den prognostizierten Wert selbst bestimmt!
Warum ultrafrische, schwer verkäufliche Produkte nicht nachhaltig angeboten werden können
Mit dieser Erkenntnis zur Fehlerskalierung im Hinterkopf kehren wir zur Frage zurück, warum frische Seegurken nicht überall auf der Welt angeboten werden: Wir zeigen die erwartete Verteilung der Verkäufe pro Tag für eine perfekte Poisson-Prognose von einer Seegurke pro Tag:

An 37 % der Tage wird es keine Nachfrage geben, an 37 % der Tage wird ein Meeresfrüchte-Liebhaber eine rohe Seegurke kaufen wollen, und an 26 % der Tage wird die Nachfrage nach zwei oder mehr Seegurken bestehen. Wie viele Seegurken sollten wir auf Lager halten, wenn wir sie am Ende des Tages wegwerfen müssen, falls sie niemand kauft? Wenn wir nur ein einziges Stück auf Lager haben, müssen wir es in 37 % der Fälle wegwerfen, während wir in 26 % der Fälle unzufriedene Kunden haben, die die Seegurke, die sie eigentlich kaufen wollten, nicht bekommen können. Da wir zwei Exemplare auf Lager haben, müssen wir nach 74 % der Tage mindestens ein Exemplar wegwerfen – welch eine Verschwendung, wenn man bedenkt, dass Seegurken vielerorts unter Schutz stehen! Offensichtlich ist ein Geschäftsmodell, das darauf abzielt, die geringe Nachfrage nach rohen Seegurken zu befriedigen, nicht rentabel und könnte nur aufrechterhalten werden, wenn die Gewinnspanne extrem hoch wäre: Die Käufer der rohen Seegurken müssten all die Tage subventionieren, an denen keine Seegurken verkauft werden – und diese Leute können nicht einmal sicher sein, dass sie eine bekommen, wenn sie eine wollen! Unter milden Annahmen hinsichtlich der Marge und der Entsorgungskosten beträgt die richtige Lagermenge für einen ultrafrischen Super-Langsamverkäufer: Null.
Auch hier liegt der Grund in der nichtproportionalen Skalierung: Die erwartete Absatzverteilung bei einer Prognose von 100 frischen Seegurken pro Tag ist nicht einfach eine aufgeblähte Version der oben genannten Verteilung für 1 Seegurke pro Tag, sondern sie hat eine andere Form – genau wie ein Elefant nicht wie eine große Impala aussieht:
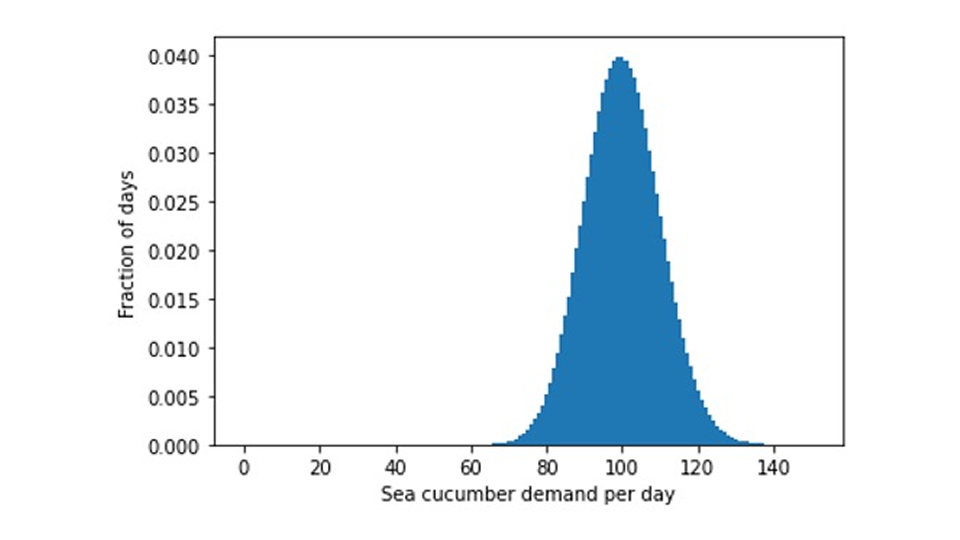
Schlechte Nachrichten für alle, die in Busan Brezeln oder in Nordeuropa eine größere Auswahl an Früchten erwartet haben! Es gibt jedoch Hoffnung: Wenn die Nachfrage eine gewisse Schwelle überschreitet, weil ein verderbliches Gericht zum Trend wird, kann sich dieses neue Lebensmittel an neuen Orten etablieren – gutes Sushi gibt es fast überall auf der Welt.
Zusammenfassend lässt sich sagen, dass aufgrund der nichtproportionalen Skalierung von Prognosefehlern die auftretenden Über- und Unterbestände eines Produkts – selbst unter der Annahme einer perfekten Prognose – überproportional ansteigen, wenn die Absatzrate sinkt. Folglich kann das Angebot bestimmter verderblicher Lebensmittel nur dann aufrechterhalten werden, wenn ab einer gewissen Absatzrate pro Haltbarkeitsdauer der richtige Preis erzielt wird.
Beurteilung des Prognosefehlers
Nachdem wir nun verstanden haben, warum wir nicht erwarten können, ausländische Delikatessen zu Hause zu finden, wollen wir nun einige Lehren für Datenwissenschaftler und Geschäftsanwender ziehen, die für die Beurteilung der Prognosequalität zuständig sind: Bei hohen prognostizierten Verkaufsraten können die zufälligen Schwankungen, die den tatsächlichen Verkaufswert im Vergleich zum prognostizierten Mittelwert nach oben oder unten treiben, nicht als Entschuldigung für eine wesentliche Abweichung dienen, und wir können eine solche Abweichung einem tatsächlichen Fehler oder Problem in der Prognose zuschreiben. Die oben besprochenen statistischen Eigenheiten spielen keine Rolle. Wenn eine Gesamtnachfrage von 1.000.000 prognostiziert wurde und der Gesamtabsatz 800.000 beträgt, ist dieser Fehler von 20 % nicht auf unvermeidbare Schwankungen zurückzuführen, sondern auf eine verzerrte Prognose.
Bei kleinen prognostizierten Zahlen können wir beobachtete Abweichungen nicht mehr eindeutig einer schlechten Prognose zuschreiben: Bei einer Prognose von eins ist die Beobachtung 0 (die zu 100 % daneben liegt) mit einer Wahrscheinlichkeit von 37 % durchaus möglich, ebenso wie die Beobachtung 2 (die ebenfalls zu 100 % daneben liegt). Die Beurteilung, ob eine Prognose gut oder schlecht ist, wird deutlich schwieriger, da die natürliche Basislinie, das unvermeidliche Rauschen, überwiegt.
Sollen wir unsere Prognosen dann in „schnelle Verkäufer“, bei denen wir beobachtete Abweichungen auf Prognosefehler zurückführen, und „langsame Verkäufer“, denen wir gegenüber wohlwollender sind, unterteilen? Davon raten wir ab: Was ist mit dem Zwischenfall, einer Vorhersage von beispielsweise 15? Wo verläuft die Grenze zwischen „langsam“ und „schnell“? Was passiert, wenn ein Produkt etwas beliebter wird, diese Grenze überschreitet und sich seine prognostizierte Qualitätsbeurteilung sprunghaft verbessert? Es gibt einen kontinuierlichen Übergang zwischen „schnell“ und „langsam“, der keine natürliche Grenze aufweist, wie wir in dieser Grafik des erwarteten relativen Fehlers einer Prognose als Funktion des prognostizierten Wertes sehen können (beachten Sie die logarithmische Skala auf der Abszisse und dass wir den erwarteten Fehler mit dem optimalen Punktschätzer berechnen, der nicht der Mittelwert, sondern der Median der Poisson-Verteilung ist):
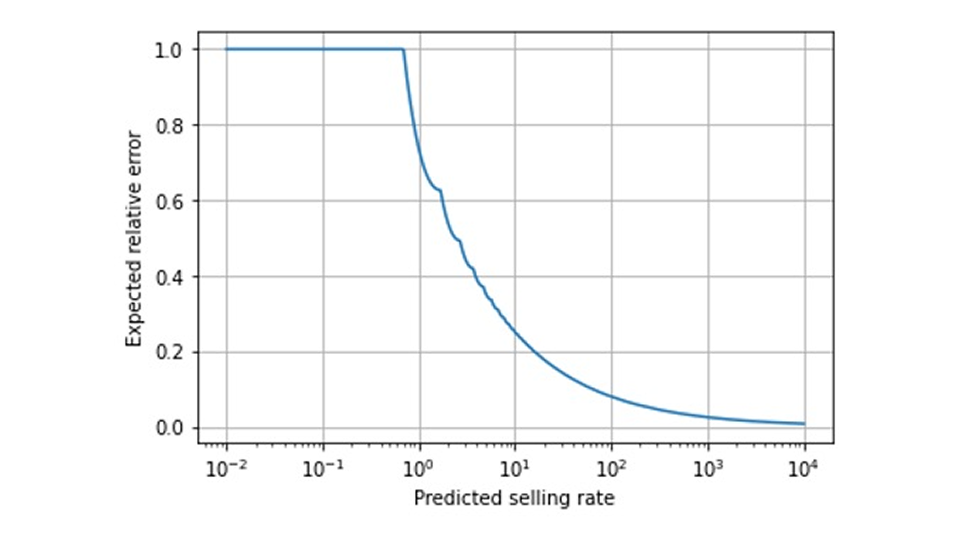
Aufgrund dieses kontinuierlichen Übergangs empfehlen wir eine stratifizierte Auswertung nach prognostizierter Rate. Dies bedeutet, dass die Prognosen in Gruppen mit ähnlichem prognostizierten Wert eingeteilt und die Fehlermetriken für jede Gruppe separat ausgewertet werden. In unserem vorherigen Blogbeitrag zum Rückschaufehler erklären wir, warum diese Kategorisierung anhand des prognostizierten Wertes und nicht anhand der tatsächlich beobachteten Verkaufszahlen erfolgen sollte, auch wenn sich letzteres natürlicher anfühlt. Für jede dieser Kategorien beurteilen wir, ob die Prognosegenauigkeit mit der theoretischen Erwartung (siehe obige Grafik) übereinstimmt oder erheblich davon abweicht. Unsere Erwartungen an eine Prognose sollten von der vorhergesagten Rate abhängen: Bei extrem kleinen Werten (kleiner als 0,69) sind die meisten beobachteten tatsächlichen Verkäufe 0, und wir liegen im Wesentlichen „immer völlig daneben“ mit einem Fehler von 100 % – unvermeidlich. Bei einer prognostizierten Verkaufsrate von 10 müssen wir – im besten Fall – mit einem erschreckend hohen relativen Fehler von 25 % leben! Bei einer Prognose von 100 = 10² erwarten wir immer noch einen relativen Fehler von etwa 8 %. Bei einer Rate von 1000 = 10³ sinkt der Fehler auf 2,5 %. Beispielsweise ist die Forderung nach einer Fehlertoleranz von 10 % über alle Verkaufsraten hinweg kontraproduktiv: Die große Mehrheit der langsamen Verkäufer wird diese Toleranzgrenze überschreiten und Ressourcen binden, um herauszufinden, warum „die Prognose nicht stimmt“, während bei den schnellen Verkäufern, die die Toleranzgrenze einhalten, noch Verbesserungen möglich sein könnten und sie daher keine Aufmerksamkeit erhalten.
In der Praxis hängt die Abweichung von der oben eingezeichneten Ideallinie vom Prognosehorizont ab (bezieht sie sich auf morgen oder auf nächstes Jahr?). und in Bezug auf die Branche (sagen wir ein bekanntes, nicht saisonabhängiges Lebensmittel voraus oder ein unkonventionelles, exquisites Kleid, das sich an der Grenze zwischen modisch und geschmacklos bewegt?). Dennoch ist die Berücksichtigung der universellen, nicht-proportionalen Skalierung von Prognosefehlern der wichtigste Aspekt, den Ihre Prognosebewertungsmethodik erfüllen sollte!
Vermeiden Sie die naive Skalierungsfalle, akzeptieren Sie den Wettbewerbsdruck durch langsame Verkäufe und gehen Sie strategisch damit um.
Abgesehen davon, dass Sie Besuche in lokalen Restaurants unbedingt auf Ihre Liste der Dinge setzen sollten, die Sie in Ihrem nächsten Urlaub tun müssen, welche Schlussfolgerungen sollten Sie aus diesem Blogbeitrag ziehen?
Stellen Sie sicher, dass die von Ihnen in Ihrer Bewertung festgelegte zeitliche Aggregationsskala mit der Zeitskala der Geschäftsentscheidung übereinstimmt: Da Erdbeeren und Seegurken nur einen Tag haltbar sind, werden sie für einen Tag eingeplant, und eine Bewertung auf Tagesebene ist angemessen. Man kann die heutige Nachfrage nach Erdbeeren nicht mit den gestrigen Überbeständen ausgleichen oder umgekehrt. Bei Artikeln, die länger halten, ist der Maßstab, auf dem sich ein Fehler bei einer Geschäftsentscheidung tatsächlich bemerkbar macht, sicherlich nicht ein Tag: Wenn ein Hemd am Montag nicht gekauft wurde, wird es vielleicht am Dienstag oder zwei Wochen später gekauft - was für den Hemdenbestand, der jeden Monat bestellt wird, keine Rolle spielt. Sollten Sie bei Ihrer Auswertung auf viele Artikel mit niedrigen prognostizierten Zahlen (<5) stoßen, überprüfen Sie noch einmal, ob es sich bei der letztgenannten Zahl tatsächlich um die relevante Zahl handelt, auf deren Grundlage eine Kauf-, Nachschub- oder sonstige Entscheidung getroffen wird.
Setzen Sie keine einheitlichen Ziele für die Prognosegenauigkeit über Ihr gesamtes Produktportfolio hinweg, weder absolut noch relativ: Ihre Verkaufsschlager erreichen problemlos niedrige relative Fehler, Ihre Ladenhüter hingegen haben scheinbar Schwierigkeiten. Teilen Sie Ihre Vorhersagen stattdessen in Gruppen mit ähnlichem Vorhersagewert ein und beurteilen Sie jede Gruppe separat. Setzen Sie sich ein realistisches, vom Absatzvolumen abhängiges Ziel.
Bei Artikeln mit geringem Absatz ist es unerlässlich, sich der Wahrscheinlichkeitsnatur von Prognosen bewusst zu sein und die großen, unvermeidbaren Schwankungen strategisch zu berücksichtigen, sei es durch Sicherheitsbestandsheuristiken im Falle von nicht verderblichen Artikeln oder durch Strategien der Produktion auf Bestellung, z. B. bei Hochzeitstorten.
Auch wenn die Unvermeidbarkeit von Prognosefehlern bei Ladenhütern ärgerlich sein mag, ist es ermutigend, dass die Grenzen der Prognosetechnologie quantitativ und auf strenge Weise ermittelt werden können, sodass wir sie strategisch in unsere Geschäftsentscheidungen einbeziehen können.













